题目内容
8.如图1,△ABE、△BCD均为直角三角形,且点E在线段BC上,∠ABC=∠BCD=90°,AB=nBE,EC=kCD,AE⊥BD于H.(1)当n=2,k=1时,求证:AE=BD;
(2)在(1)的条件下,求tan∠BCH的值;
(3)如图2,当AE平分BD时,请直接写出k=0(用含n的代数式表示).
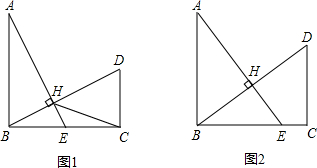
分析 (1)由∠ABC=∠BCD=90°,AE⊥BD,于是得到∠A+∠ABH=∠ABH+∠DBC,证得∠A=∠DBC,由于tanA=tan∠DBC=$\frac{BE}{AB}$=2,证得CD=BE,于是得到△ABE≌△BCD,即可得到结论;
(2)设BE=1,则AB=n,根据勾股定理可得AE=$\sqrt{{n}^{2}+1}$,由(1)证得△ABE≌△BCD,于是得到CD=BE=1,BC=AB=n,根据三角形的面积公式得到BH=$\frac{AB•BE}{AE}$=$\frac{1}{\sqrt{{n}^{2}+1}}$,求得HD=BD-BH=AE-BH=$\sqrt{{n}^{2}+1}$-$\frac{1}{\sqrt{{n}^{2}+1}}$=$\frac{{n}^{2}}{\sqrt{{n}^{2}+1}}$,如图1,延长CH交AB于点M,证得△MHB∽△CHD,求得MB=$\frac{1}{{n}^{2}}$,即可得到结果;
(3)当AE平分BD时,即BH=HD,即$\frac{1}{\sqrt{{n}^{2}+1}}$=$\frac{{n}^{2}}{\sqrt{{n}^{2}+1}}$,求得n=1(负值舍去),由于EC=kCD,即BC-BE=kCD,得到k=0,此时△ABE和△BCD均为等腰直角三角形,点E与点C重合.
解答 解:(1)∵∠ABC=∠BCD=90°,AE⊥BD,
∴∠A+∠ABH=∠ABH+∠DBC,
∴∠A=∠DBC,
∵tanA=tan∠DBC=$\frac{BE}{AB}$=2,
∴BC=2CD,
∵CD=CE,
∴CD=BE,
在△ABE与△BCD中,
$\left\{\begin{array}{l}{∠A=∠DBC}\\{∠ABC=∠BCD}\\{BE=CD}\end{array}\right.$,
∴△ABE≌△BCD,
∴AE=BD;
(2)设BE=1,则AB=n,根据勾股定理可得AE=$\sqrt{{n}^{2}+1}$,
由(1)证得△ABE≌△BCD,
∴CD=BE=1,BC=AB=n,
∵AH⊥BD,
∴S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$AE•BH,
∴BH=$\frac{AB•BE}{AE}$=$\frac{1}{\sqrt{{n}^{2}+1}}$,
∴HD=BD-BH=AE-BH=$\sqrt{{n}^{2}+1}$-$\frac{1}{\sqrt{{n}^{2}+1}}$=$\frac{{n}^{2}}{\sqrt{{n}^{2}+1}}$,
如图1,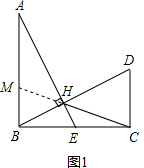 延长CH交AB于点M,
延长CH交AB于点M,
∵∠ABC=∠BCD=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD,
∴△MHB∽△CHD,
∴$\frac{MB}{CD}=\frac{BH}{CD}$,
即$\frac{MB}{1}=\frac{1}{{n}^{2}}$,
∴MB=$\frac{1}{{n}^{2}}$,
∴tan∠BCH=$\frac{MB}{BC}$=$\frac{MB}{AB}$=$\frac{1}{{n}^{3}}$;
(3)当AE平分BD时,
即BH=HD,
即$\frac{1}{\sqrt{{n}^{2}+1}}$=$\frac{{n}^{2}}{\sqrt{{n}^{2}+1}}$,
∴n=1(负值舍去),
∵EC=kCD,
即BC-BE=kCD,
即n-1=k•1,
∴k=0,
此时△ABE和△BCD均为等腰直角三角形,点E与点C重合.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰直角三角形的判定,正确的作出辅助线是解题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案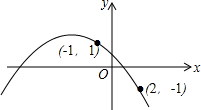 如图,二次函数y=ax2+bx+c(a<0)的图象过(-1,1)、(2,-1)两点,下列关于此二次函数的叙述中,正确的有( )
如图,二次函数y=ax2+bx+c(a<0)的图象过(-1,1)、(2,-1)两点,下列关于此二次函数的叙述中,正确的有( )①y的最大值小于0
②当x=0时,y的值大于1
③当x=1时,y的值大于1
④当x=3时,y的值小于0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 数轴上的点与实数一一对应 | B. | 实数中没有最小的数 | ||
| C. | a、b为实数,若a<b,则$\sqrt{a}$<$\sqrt{b}$ | D. | a、b为实数,若a<b,则$\root{3}{a}$<$\root{3}{b}$ |