题目内容
15.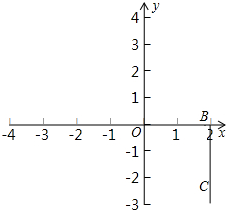 如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).
如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).(1)求D点的坐标.
(2)将这个长方形向左平移1个单位长度,然后再向上平移2个单位长度,得到长方形A′B′C′D.画出平移后的图形,并指出其各个顶点的坐标.
(3)求△D′B′C的面积.
分析 (1)根据题意画出图形,根据点D在坐标系中的位置即可得出结论;
(2)画出平移后的图形,并写出其各个顶点的坐标即可;
(3)先利用待定系数法求出直线B′C的解析式,进而得出E点坐标,利用S△D′B′C=S△B′D′E+S△D′EC即可得出结论.
解答 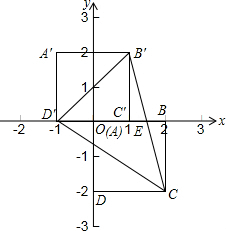 解:(1)D(0,-2);
解:(1)D(0,-2);
(2)由图可知,A′(-1,2),B′(1,2),C′(1,0),D′(-1,0);
(3)设平移后,B′C与x轴交于点E,直线B′C的解析式为y=kx+b(k≠0),
∵B′(1,2),C(2,-2),
∴$\left\{\begin{array}{l}k+b=2\\ 2k+b=-2\end{array}\right.$,
解得$\left\{\begin{array}{l}k=-4\\ b=2\end{array}\right.$.
∴直线B′C的解析式为y=-4x+2,当y=0时,x=2,即E(2,0),
D′E=2-(-1)=3,
∴S△D′B′C=$\frac{1}{2}$D′E×2+$\frac{1}{2}$D′E×2=3+3=6.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目