题目内容
2.(1)已知$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+cy=1}\\{cx-by=2}\end{array}\right.$的解,写出a、b的关系式.(2)解方程:$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1.
分析 (1)将方程组的解入方程组得:$\left\{\begin{array}{l}{-3a-2c=1}\\{-3c+2b=2}\end{array}\right.$,然后将-3a-2c=1变形得:c=$-\frac{1}{2}$(1+3a)③,将③代入-3c+2b=2得:$\frac{3}{2}(1+3a)+2b=2$,整理得:9a+4b=1;
(2)方程两边同时乘以x2-1,将分式方程转化为整式方程,然后解整式方程求得方程组的解,然后进行检验即可.
解答 解:(1)将$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{-3a-2c=1}\\{-3c+2b=2}\end{array}\right.$,
由-3a-2c=1得:c=$-\frac{1}{2}$(1+3a)③,将③代入-3c+2b=2得:$\frac{3}{2}(1+3a)+2b=2$,
整理得:9a+4b=1;
(2)方程两边同时乘以x2-1得:(x+1)2-4=x2-1,
整理得:2x=2
解得:x=1,
将x=1代入(x2-1)=0,
∴x=1是原方程的增根.
∴原方程无解.
点评 本题主要考查的方程组的解和解分式方程,掌握方程的解的定义和解分式方程的步骤和方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
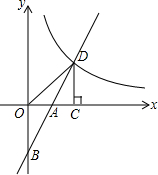 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,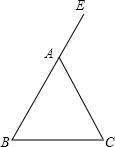 如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.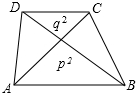 如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.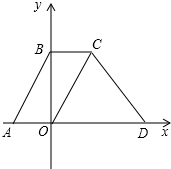 如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.