题目内容
10.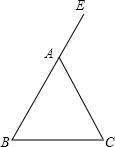 如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.(1)利用尺规∠EAC的平分线AD(保留作图痕迹,不写作法);
(2)若点P在射线AD上从点A开始运动,点Q在线段CB上从点C向点点B运动,运动的速度均为1cm/s,运动时间为t,若P、Q同时运动.
①连接PQ交AC于点O.求证:AO=CO;
②填空:当t=6秒时四边形APCQ一定是矩形;
③填空:当t=$\frac{25}{3}$秒时四边形APCQ一定是菱形.
分析 (1)利用尺规作图作出已知角的平分线即可;
(2)根据平行四边形的性质、矩形的性质及菱形的性质分别求得t的值即可.
解答 解:(1)作图如下:

(2)①∵AP平分∠EAC,∠EAC=2∠B=2∠C,
∴∠PAC=∠C,
∴AP∥BC,
∵点P和点Q的速度均为1cm/s,
∴AP=CQ,
∴AO=CO;
②∵当∠AQC=90°时,四边形AQCP为矩形,
此时AQ⊥BC,CQ=$\frac{1}{2}$BC=6,
∴当t=6时,四边形AQCP为矩形;
③如图3:当四边形APCQ是菱形时,AQ=CQ,
作AD⊥CQ于点D,
则CD=$\frac{1}{2}$BC=6,
CQ=AQ=t,QD=t-6,
在Rt△AQD中,
AQ2=QD2+AD2,
即:t2=(t-6)2+82,
解得:t=$\frac{25}{3}$,
∴当t=$\frac{25}{3}$时,四边形AQCP为菱形.
点评 考查了菱形的判定、等腰三角形的性质及矩形的判定,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.

练习册系列答案
相关题目
1.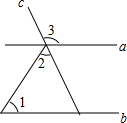 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
5.某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
| A. | 3900(1+x)2=2500 | B. | 3900(1-x)2=2500 | C. | 3900(1-2x)=2500 | D. | 2500(1+x)2=3900 |
19.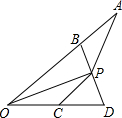 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.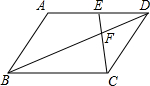 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
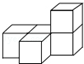 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )
如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )