题目内容
7.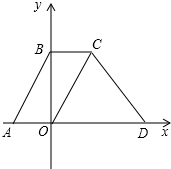 如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.(1)求m的值;
(2)点P(0,t)是线段OB上的一个动点(点P不与0,B两点重合),过点P作x轴的平行线,分别交AB,OC,DC于点E,F,G,设线段EG的长为d,求d与t之间的函数关系式并直接写出自变量t的取值范围.
分析 (1)首先求得A和B的坐标,过C作CK⊥x轴于K,则四边形BOKC是矩形,求得C的坐标,即可求得CK的长,即OB的长,从而求得m的值;
(2)延长DC交y轴于点N,分别过点E、G作x轴的垂线,垂足为R和Q.则四边形ERQG、四边形POQG、四边形EROP都是矩形,根据△ARE∽△AOB,即可求得AR的值,则函数解析式即可求解.
解答 解:(1)∵当x=0时,y=4,
∴点B的坐标是(0,4),OB=4,
由2x+4=0,解得x=-2,
∴A的坐标是(-2,0),OA=2,
∵四边形ABCO是平行四边形,过C作CK⊥x轴于K.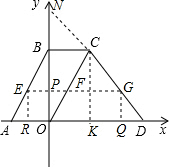
则四边形BOKC是矩形,
∴OK=BC=2,CK=OB=4,
∴点C的坐标是(2,4).
∴4=-2+m,
∴m=6;
(2)延长DC交y轴于点N,分别过点E、G作x轴的垂线,垂足为R和Q.
则四边形ERQG、四边形POQG、四边形EROP都是矩形,
∴ER=PO=GQ=t,
∵△ARE∽△AOB,
∴$\frac{ER}{AR}=\frac{OB}{OA}$,
∴$\frac{t}{AR}=\frac{4}{2}$,
∴AR=$\frac{1}{2}$t,
∵OD=ON=6,
∴∠ODN=45°,
∴DQ=GQ=t,
又AD=AO+OD=8,
∴EG=RQ=8-$\frac{1}{2}$t-t=8-$\frac{3}{2}$t,
∴d=-$\frac{3}{2}$t+8(0<t<4).
点评 本题考查了平行四边形的性质,以及相似三角形的判定与性质,正确作出辅助线,利用t表示出AR是关键.

练习册系列答案
相关题目
17.下列各数中,最大的数是( )
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 1 |
19.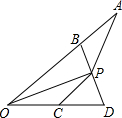 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.如果命题P成立能得到命题Q成立,那么下列说法正确的是( )
| A. | P不成立,则Q不成立 | B. | Q成立,则P成立 | ||
| C. | Q不成立,则P不成立 | D. | 以上三种说法均错误 |
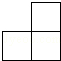
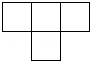
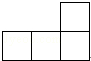
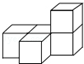 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )
如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )


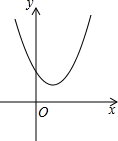 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.