题目内容
17.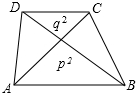 如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
分析 过O作OE⊥CD于E,延长EO交AB于F,则EF为梯形ABCD的高,根据△COD和△AOB的面积可以求得AB、CD的值,根据AB、CD、EF的值即可计算梯形ABCD的面积,即可解题.
解答 解:∵四边形ABCD是梯形,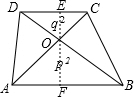
∴AB∥CD,
如图,过O作OE⊥CD于E,延长EO交AB于F,
则EF⊥AB,
∴△ABO∽△CDO,
∴$\frac{CD}{AB}=\frac{OE}{OF}=\sqrt{\frac{{S}_{△CDO}}{{S}_{△ABO}}}$=q:p,
设上下底分别为mq,mp,两个三角形对应的高分别为nq,np,
有$\frac{mp•np}{2}$=p2,得mn=2
∴S梯形ABCD=$\frac{(mp+mq)(np+nq)}{2}$=$\frac{mn(p+q)^{2}}{2}$=(p+q)2,
故答案为:(p+q)2.
点评 本题考查了相似三角形的判定和性质,梯形面积的计算,考查了直角三角形中勾股定理的运用,本题中求EF的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.“低碳生活,绿色出行”,电动汽车将逐渐代替燃油汽车,成为人们出行的主要交通工具,某城市一汽车销售4S店,今年2月份销售电动汽车共计64辆,4月份销售电动汽车共计100辆.若每月汽车销售增长率相同,则该汽车销售4S店5月份能销售电动汽车( )辆.
| A. | 111 | B. | 118 | C. | 125 | D. | 132 |
5.某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
| A. | 3900(1+x)2=2500 | B. | 3900(1-x)2=2500 | C. | 3900(1-2x)=2500 | D. | 2500(1+x)2=3900 |
12.把ax2-4ay2分解因式正确的是( )
| A. | a(x+2y)(x-2y) | B. | a(x-2y)2 | C. | a(x-4y)2 | D. | a(x+4y)(x-4y) |
 如图,边长为1的正六边形ABCDEF内接于⊙O,则图中阴影部分图形的面积是$\frac{π}{3}$(结果保留π)
如图,边长为1的正六边形ABCDEF内接于⊙O,则图中阴影部分图形的面积是$\frac{π}{3}$(结果保留π)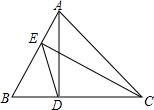 如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,△ABC的面积是△BDE面积的4倍,AC=6,求DE的长.
如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,△ABC的面积是△BDE面积的4倍,AC=6,求DE的长.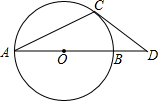 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.
如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.