题目内容
2.已知:一次函数y=x-2与反比例函数y=$\frac{{m}^{2}}{x}$(m≠0).(1)求证:这两个函数的图象一定有两个不同的交点;
(2)若他们的一个交点是(1,m),求反比例函数的解析式.
分析 (1)将两个函数解析式联立后,通过方程x2-2x-m2=0的判别式判断方程总有两个不相等的实数根,再进行证明;
(2)将点A分别代入两个函数解析式,继而即可求出m的值.
解答 解:(1)证明:把y=x-2代入y=$\frac{{m}^{2}}{x}$得x-2=$\frac{{m}^{2}}{x}$,
整理得:x2-2x-m2=0,
∵△=4+4m2,且m≠0,
∴4+4m2>0,
∴方程x2-2x-m2=0有两个不相等的实数根,
∴这两个函数的图象一定有两个不同的交点;
(2)把x=1,y=m代入y=x-2得,m=-1,
故反比例函数的解析式为y=$\frac{1}{x}$.
点评 本题考查了反比例函数与一次函数的交点问题,难度适中,注意掌握求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.一次函数y=4x+1,当x>0时,y的取值范围为( )
| A. | y>0 | B. | y<0 | C. | y>1 | D. | 0<y<1 |
13.若关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=-4,则m+n的值是( )
| A. | -10 | B. | 10 | C. | -6 | D. | -1 |
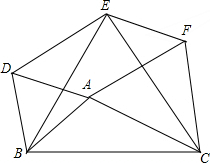 如图所示,以△ABC的三边AB、BC、CA在BC的同侧作等边△ABD、△BCE、△CAF
如图所示,以△ABC的三边AB、BC、CA在BC的同侧作等边△ABD、△BCE、△CAF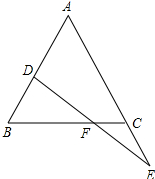 已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.
已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.