题目内容
2．解方程组：$\left\{\begin{array}{l}{x+y-3z=12}\\{4x-y+z=10}\\{x+5y-z=8}\end{array}\right.$．分析 先②+③和①+②×3消去z，再利用二元一次方程组解答即可．
解答 解：$\left\{\begin{array}{l}{x+y-3z=12①}\\{4x-y+z=10②}\\{x+5y-z=8③}\end{array}\right.$，
②+③得：5x+4y=18④，
①+②×3得：13x-2y=42⑤，
④+⑤×2得：x=$\frac{102}{31}$，
把x=$\frac{102}{31}$代入④得：y=12，
把x=$\frac{102}{31}$，y=12代入③得：z=$55\frac{9}{31}$，
所以方程组的解是：$\left\{\begin{array}{l}{x=\frac{102}{31}}\\{y=12}\\{z=55\frac{9}{31}}\end{array}\right.$
点评 此题考查三元一次方程组，关键是利用加减消元计算．
练习册系列答案
名校课堂系列答案
相关题目
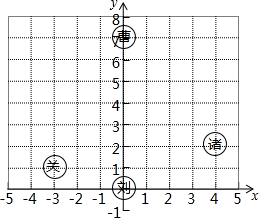三国时期的一次战役中，曹军的位置在（0，7），蜀军的3支部队位置如图所示，诸葛亮安排关羽先向北然后向东移动刘备向北移动，张飞先向北再向西移动，从三面围击曹军．
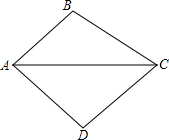如图，已知△ABC经过变换能够与△ADC重合，∠BAC=50°，∠ACD=33°．
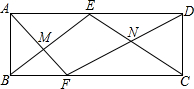如图，矩形ABCD中，点E、F分别在边AD、BC上，AF、BE交于M，DF、CE交于N，且△AME的面积是4，△BMF的面积是2，△DCN的面积是3．则矩形EMFN的面积是2$\sqrt{2}$+3．
如图，?ABCD中，点O是AC与BD的交点，过点O的直线与BA、DC的延长线分别交于点E、F．