题目内容
20.盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时,猜中的可能性大.请说明理由.
分析 (1)将所有等可能的结果列举出来,利用三角形的三边关系进行判断后利用概率公式进行计算即可;
(2)确定和为5的概率最大即可得到猜和为多少时猜中的可能性大.
解答 解:(1)从盒中取三个球,共有1、2、3,1、2、4,1、3、4,2、3、4四种情况
其中能构成三角形的只有2、3、4这一种情况.故P(构成三角形)=$\frac{1}{4}$;(3分)
(2)由题意小华猜和为5时,猜中的可能性大,因为数字5出现的概率最大,为$\frac{1}{4}$.
点评 本题考查了列表与树状图法求概率及三角形的三边关系的知识,解题的关键是能够确定所有等可能的结果,难度不大.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | -$\sqrt{0.64}$=0.8 | C. | ±$\sqrt{0.81}$=±0.9 | D. | -$\sqrt{49}$=±7 |
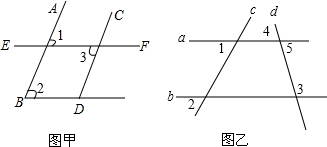 (1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由:
(1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由: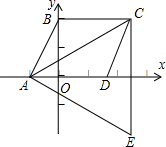 如图,已知△ACE是以平行四边形ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若点E的坐标是(7,$-3\sqrt{3}$),则点D的坐标是(5,0).
如图,已知△ACE是以平行四边形ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若点E的坐标是(7,$-3\sqrt{3}$),则点D的坐标是(5,0).