题目内容
13.已知直线l:y=ax-a-2,其中a为实数(常数),可知直线l必经过定点(1,-2);过点P(-1,0)作直线l的垂线,垂足为M,点O为坐标原点,则线段OM长度的最小值为$\sqrt{2}$-1,最大值为$\sqrt{2}$+1.分析 对于任意实数a,直线l必经过定点,所以a的系数为0,据此可求得该定点,以定点和P点间的线段为圆心,以线段的长为直径,交y轴于M1、M2,则OM1是OM的最小值,OM2是OM的最大值.
解答 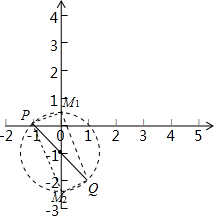 解:∵y=ax-a-2=(x-1)a-2,
解:∵y=ax-a-2=(x-1)a-2,
∴当a的系数x-1=0,即x=1时,
对于任意实数a,直线y=ax-a-2,都经过应该定点Q(1,-2),
如图,以P(-1,0)和Q(1,-2)之间的线段为直径画弧,交y轴于M1、M2,则OM1最小,OM2z最大,
∵P(-1,0),Q(1,-2),
∴PQ=$\sqrt{(-1+1)^{2}+(0-2)^{2}}$=2$\sqrt{2}$,
∴圆心为(0,-1),半径为$\sqrt{2}$,
∴OM1=$\sqrt{2}$-1,OM2=$\sqrt{2}$+1,
∴OM长度的最小值为 $\sqrt{2}$-1,最大值为 $\sqrt{2}$+1.
故答案为1,-2、$\sqrt{2}$-1、$\sqrt{2}$+1.
点评 本题考查了一次函数图象上点的坐标特征,解题时要关键把握住a的系数为0.

练习册系列答案
相关题目
8.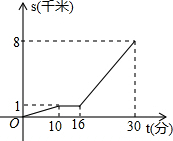 小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
 小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )| A. | 他家到公交车站台为1千米 | B. | 他等公交车的时间为6分钟 | ||
| C. | 他步行的速度100米/分钟 | D. | 公交车的速度是350米/分钟 |
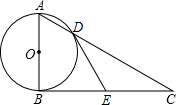 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接BD、DE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接BD、DE.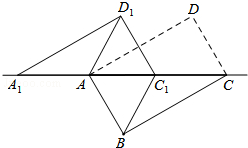 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论: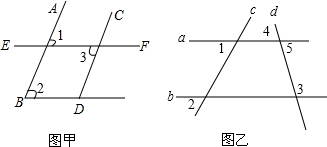 (1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由:
(1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由: