题目内容
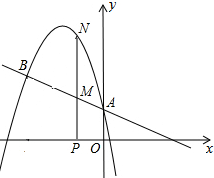 如图,二次函数y=-
如图,二次函数y=-| 5 |
| 4 |
| 1 |
| 2 |
(1)求二次函数解析式;
(2)求点B坐标;
(3)点N是二次函数上一点(点N在线段AB上方),过N作NP⊥x轴垂足为点P,交AB于M,求MN最大值.
考点:二次函数综合题
专题:
分析:(1)首先求得A的坐标,然后利用待定系数法即可求得二次函数的解析式;
(2)根据求得的二次函数的解析式和直线的解析式求得交点坐标即可求得点B的坐标;
(3)设M的横坐标是x,则根据M和N所在函数的解析式,即可利用x表示出M、N的坐标,利用x表示出MN的长,利用二次函数的性质求解.
(2)根据求得的二次函数的解析式和直线的解析式求得交点坐标即可求得点B的坐标;
(3)设M的横坐标是x,则根据M和N所在函数的解析式,即可利用x表示出M、N的坐标,利用x表示出MN的长,利用二次函数的性质求解.
解答:解:(1)由直线y=-
x+1可知A(0,1),又点(-1,4)经过二次函数,
根据题意得:
,
解得:
,
则二次函数的解析式是:y=-
x2-
x+1;
(2)∵y=-
x2-
x+1与直线y=-
x+1相交于点A、B,
∴-
x2-
x+1=-
x+1,
解得:x=0或x=-3,
∴y=1或y=
,
∴B(-3,
);
(3)设N(x,-
x2-
x+1),
则M(x,-
x+1),P(x,0).
∴MN=PN-PM
=-
x2-
x+1-(-
x+1)
=-
x2-
x
=-
(x+
)2+
,
则当x=-
时,MN的最大值为
;
| 1 |
| 2 |
根据题意得:
|
解得:
|
则二次函数的解析式是:y=-
| 5 |
| 4 |
| 17 |
| 4 |
(2)∵y=-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
∴-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
解得:x=0或x=-3,
∴y=1或y=
| 5 |
| 2 |
∴B(-3,
| 5 |
| 2 |
(3)设N(x,-
| 5 |
| 4 |
| 17 |
| 4 |
则M(x,-
| 1 |
| 2 |
∴MN=PN-PM
=-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
=-
| 5 |
| 4 |
| 15 |
| 4 |
=-
| 5 |
| 4 |
| 3 |
| 2 |
| 45 |
| 16 |
则当x=-
| 3 |
| 2 |
| 45 |
| 16 |
点评:本题是待定系数法求二次函数的解析式,以及二次函数的性质的综合应用,利用二次函数的性质可以解决实际问题中求最大值或最小值问题.

练习册系列答案
相关题目
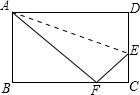 如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度?
如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度? 在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.
在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.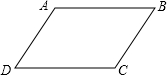 如图所示,已知AB=CD,BC=DA,求证:AB∥CD,BC∥DA.
如图所示,已知AB=CD,BC=DA,求证:AB∥CD,BC∥DA. 如图,∠AOC=∠BOD=90°,且∠AOB=162°,则∠COD=
如图,∠AOC=∠BOD=90°,且∠AOB=162°,则∠COD=
 如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.