题目内容
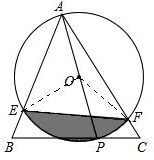
 在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.
在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.(1)若∠BAC=45°,EF=4,则AP的长为多少?
(2)在(1)条件下,求阴影部分面积.
(3)若∠ABC=60°,∠BAC=45°,AB=4
| 3 |
考点:圆的综合题,垂线段最短,勾股定理,扇形面积的计算,锐角三角函数的定义
专题:综合题
分析:(1)连接OE、OF,由圆周角定理可得∠EOF=2∠EAF=90°,然后利用勾股定理可求得OE的长,就可得到AP的长;
(2)利用扇形和三角形的面积公式,运用割补法即可求出阴影部分的面积;
(3)由EF=
OE可知,当AP最短时,OE最短,EF也就最短;根据“点到直线之间垂线段最短”可知,当AP⊥BC时,AP最短,在Rt△APB中,利用三角函数即可求出AP的长,从而得到OE的长,进而得到EF的长.
(2)利用扇形和三角形的面积公式,运用割补法即可求出阴影部分的面积;
(3)由EF=
| 2 |
解答:解:(1)连接OE、OF.
∵∠EAF=45°,
∴∠EOF=2∠EAF=90°.
∵OE=OF,EF=4,
∴EF=
=
OE=4,
∴OE=2
,
∴直径AP=2OE=4
;
(2)S阴影=S扇形OEF-S△EOF
=
-
×2
×2
=2π-4,
∴阴影部分面积为2π-4;
(3)由EF=
OE可知,当AP最短时,OE最短,EF也就最短;
根据“点到直线之间垂线段最短”可知,当AP⊥BC时,AP最短.
此时,∵∠ABC=60°,AB=4
,
∴AP=AB•sin∠ABC=4
×
=6,
∴OE=
AP=3,
∴EF=
OE=3
,
∴线段EF的最小值为3
.
∵∠EAF=45°,
∴∠EOF=2∠EAF=90°.
∵OE=OF,EF=4,
∴EF=
| OE2+OF2 |
| 2 |
∴OE=2
| 2 |

∴直径AP=2OE=4
| 2 |
(2)S阴影=S扇形OEF-S△EOF
=
90•π•(2
| ||
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
=2π-4,
∴阴影部分面积为2π-4;
(3)由EF=
| 2 |
根据“点到直线之间垂线段最短”可知,当AP⊥BC时,AP最短.
此时,∵∠ABC=60°,AB=4
| 3 |
∴AP=AB•sin∠ABC=4
| 3 |
| ||
| 2 |
∴OE=
| 1 |
| 2 |
∴EF=
| 2 |
| 2 |
∴线段EF的最小值为3
| 2 |
点评:本题主要考查了圆周角定理、勾股定理、扇形的面积公式、点到直线之间垂线段最短、三角函数等知识,运用割补法是解决第(2)小题的关键,利用EF=
OE及点到直线之间垂线段最短是解决第(3)小题的关键.
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、泸 | D、州 |
 如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且
如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且 据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.
据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.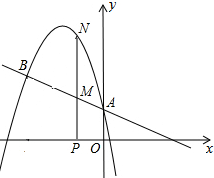 如图,二次函数y=-
如图,二次函数y=- 如图,化简|a+b|-|a|+|b|=
如图,化简|a+b|-|a|+|b|=