题目内容
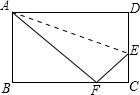如图，长方形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF=55°，则∠AEF为多少度？考点：翻折变换（折叠问题）
专题：
分析：借助翻折变换的性质证明∠DAF+∠DEF=180°；求出∠DAF的度数即可解决问题．
解答：解：由题意得：
△ADE≌△AFE，
∴∠AFE=∠D=90°；
∠AED=∠AEF，
∴∠DAF+∠DEF=360°-180°=180°；
∴∠AEF=
；
∵四边形ABCD为矩形，且∠BAF=55°，
∴∠DAF=90°-55°=35°；
∴∠AEF=72.5°；
即∠AEF为72.5°．
解：由题意得：△ADE≌△AFE，
∴∠AFE=∠D=90°；
∠AED=∠AEF，
∴∠DAF+∠DEF=360°-180°=180°；
∴∠AEF=
| 180°-∠DAF |
| 2 |
∵四边形ABCD为矩形，且∠BAF=55°，
∴∠DAF=90°-55°=35°；
∴∠AEF=72.5°；
即∠AEF为72.5°．
点评：该命题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活借助翻折变换的性质等几何知识求出有关线段或角的值；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
如图经过原点的抛物线y=ax2+bx经过点A、B两点，其中OB=12，且
据绝对值的几何意义，方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值．在数轴上，1和-2的距离之和为3，所以满足方程的x的对应点在1的右边或-2的左边；若x对应点在1的右边，由图可看出x=2；同时，若x对应点在-2的左边，可得x=-3，所以原方程的解是x=2或x=-3．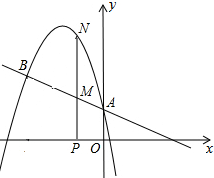
如图，二次函数y=-
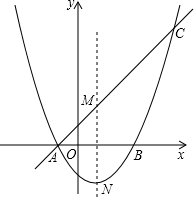如图，抛物线y=