题目内容
5.观察下列各式:$\frac{1}{2}$=$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{6}$=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{12}$=$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,$\frac{1}{20}$=$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,$\frac{1}{30}$=$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$,…(1)请你根据上面各式的规律,写出符合该规律的一道等式:$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$
(2)请利用上述规律计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$
(用含有n的式子表示)
(3)请利用上述规律解方程:$\frac{1}{(x-2)(x-1)}$+$\frac{1}{(x-1)x}$+$\frac{1}{x(x+1)}$=$\frac{1}{x+1}$.
分析 (1)观察已知等式得出规律,写出即可;
(2)利用得出的拆项规律得出结果即可;
(3)分式方程利用拆项法变形后,求出解即可.
解答 解:(1)$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$(答案不唯一);
故答案为:$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$;
(2)原式=$\frac{n}{n+1}$;
故答案为:$\frac{n}{n+1}$
(3)分式方程整理得:$\frac{1}{x-2}$-$\frac{1}{x-1}$+$\frac{1}{x-1}$-$\frac{1}{x}$+$\frac{1}{x}$-$\frac{1}{x+1}$=$\frac{1}{x+1}$,
即$\frac{1}{x-2}$=$\frac{2}{x+1}$,
方程两边同时乘(x-2)(x-1),得x+1=2(x-2),
解得:x=5,
经检验,x=5是原分式方程的解.
点评 此题考查了解分式方程,约分,以及列代数式,弄清拆项的方法是解本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.-5的相反数等于( )
| A. | -5 | B. | 5 | C. | ±5 | D. | 无法确定 |
14.若-1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果( )
| A. | 2x-1 | B. | -2x+1 | C. | 3 | D. | -3 |
 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.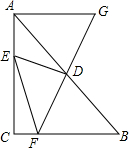 如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连接EF、AG,已知AB=10,BC=6,AC=8.
如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连接EF、AG,已知AB=10,BC=6,AC=8. 如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD.
如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD.