题目内容
15．
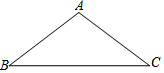如图，△ABC中，AB=AC．（1）请利用直尺和圆规作∠BAC的平分线，交BC于点D．
（2）若AB=10，AD=6，求BC的长．
分析 （1）利用直尺和圆规作∠BAC的平分线，交BC于点D即可；
（2）先根据等腰三角形的性质得出AD⊥BC，BC=2BD，进而可得出结论．
解答 
解：（1）如图，AD即为所求；
（2）∵AB=AC，AD平分∠BAC，
∴AD⊥BC，BC=2BD．
∵AB=10，AD=6，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=6，
∴BC=2BD=12．
点评 本题考查的是作图-基本作图，熟知角平分线的作法及等腰三角形的性质是解答此题的关键．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
3．
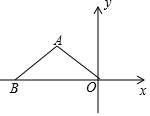如图，已知等腰△ABO的底边BO在x轴上，且BO=8，AB=AO=5，点A的坐标是（ ）
如图，已知等腰△ABO的底边BO在x轴上，且BO=8，AB=AO=5，点A的坐标是（ ）| A． | （-3，4） | B． | （3，-4） | C． | （-4，3） | D． | （4，-3） |
20．点M（cos30°，sin30°）关于原点中心对称的点的坐标是（ ）
| A． | （$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$） | C． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | D． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$） |
7．在Rt△ABC中，∠C=90°，a=1，b=$\sqrt{3}$，则∠A=（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |