题目内容
5.?ABCD中,∠A=30°,AB边上的高为6,则BC的长为( )| A. | 12 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 6$\sqrt{3}$ |
分析 由含30°角的直角三角形的性质得到AD的长,再根据平行四边形的性质即可得到结论.
解答 解:如图,过D作DE⊥AB于E,
则DE=6,∠AED=90°,
∵∠A=30°,
∴AD=2DE=12,
∵四边形ABCD是平行四边形,
∴BC=AD=12,
故选A.
点评 本题考查了平行四边形的性质,含30°角的直角三角形的性质;熟练掌握平行四边形的性质,由含30°角的直角三角形的性质求出AD是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15.下列多项式中,不能用平方差公式分解的是( )
| A. | -m4-n4 | B. | -16x2+y2 | C. | 1.96-x2 | D. | $\frac{1}{9}$a2-$\frac{1}{4}$b2 |
13.若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{1-2x>x-2}\end{array}\right.$有三个整数解,则实数a的取值范围是( )
| A. | 2≤a≤3 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 2<a<3 |
20.已知点A(a+3,4-a)在y轴上,则点A的坐标为( )
| A. | (0,1) | B. | (0,7) | C. | (0,-7) | D. | (7,0) |
10. 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 8 |
14.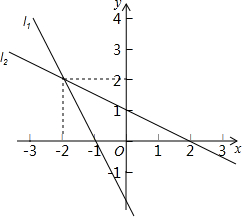 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
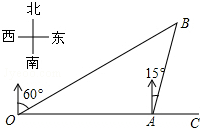 如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.