题目内容
2.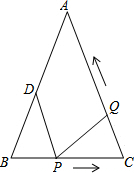 如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.(1)证明:∠B=∠C;
(2)若点P的速度是3cm/s,点Q的运动速度与点P的运动速度相等,则t为何值时△BPD与△CQP全等?请说明理由;
(3)若点P的速度比点Q的速度慢1cm/s,则点Q的运动速度为多少时,能使△BPD与△CQP全等?请说明理由.
分析 (1)根据全等三角形的判定和性质即可得到结论;
(2)求出BP、CQ、CP,根据全等三角形的判定推出即可;
(3)设当点Q的运动速度为x厘米/时,点P的速度是(x-1)cm/s,时间是t小时,能够使△BPD与△CQP全等,求出BD=5厘米,BP=(x-1)t厘米,CP=[8-(x-1)t]厘米,CQ=xt厘米,∠B=∠C,根据全等三角形的性质得出方程,求出方程的解即可.
解答 解:(1)过A作AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD与Rt△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD,
∴∠B=∠C;
(2)点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP全等,
理由是:∵AB=AC=10厘米,点D为AB的中点,
∴∠B=∠C,BD=5厘米,
∵BP=CQ=3t厘米=3厘米,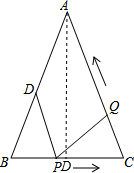
∴CP=8厘米-3厘米=5厘米=BD,
在△DBP和△PCQ中,
$\left\{\begin{array}{l}{BD=CP}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$,
∴△DBP≌△PCQ(SAS);
(3)设当点Q的运动速度为xcm/s,点P的速度是(x-1)cm/s,时间是t小时,能够使△BPD与△CQP全等,
∵BD=5厘米,BP=(x-1)t厘米,CP=[8-(x-1)t]厘米,CQ=xt厘米,∠B=∠C,
∴当BP=CQ,BD=CP或BP=CP,BD=CQ时,△BPD与△CQP全等,
即①(x-1)t=xt,5=8-(x-1)t(不合题意,舍去),
②(x-1)t═8-(x-1)t,5=xt,
解得:x=5,
即当点Q的运动速度为5厘米/时时,能够使△BPD与△CQP全等.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,特别是利用分类讨论的方法讨论三角形全等的情况,培养学生综合解题的能力.

 阅读快车系列答案
阅读快车系列答案| A. | 2≤a≤3 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 2<a<3 |
 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 8 |
| 个人旅游年消费金额x/元 | x≤2000 | 2000<x≤4000 | 4000<x≤6000 | 6000<x≤8000 | 8000<x≤10000 |
| 频数 | 12 | 25 | 31 | 22 | 10 |
| A. | 小王随机抽取了100名员工 | |
| B. | 在频数分布表中,组距是2000,组数是5组 | |
| C. | 个人旅游年消费金额在6000元以上的人数占随机抽取人数的22% | |
| D. | 在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有37人 |
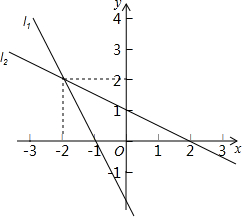 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
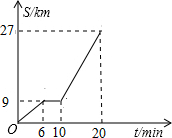 如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题: