题目内容
16.已知函数y=x2-|x-2|的图象与x轴相交于A、B两点,另一条抛物线y=ax2-2x+4也过A、B两点,则a=-2.分析 分x>2和x<2两种情况解出方程,求出A、B两点的坐标,把点A的坐标代入另一条抛物线,求出a的值即可.
解答 解:当x>2时,函数y=x2-|x-2|可化为y=x2-x+2,
x2-x+2=0,方程无解,
当x<2时,函数y=x2-|x-2|可化为y=x2+x-2,
x2+x-2=0,x1=-2,x2=1,
则A(-2,0),B(1,0),
4a+4+4=0,
解得a=-2.
故答案为:-2.
点评 本题考查的是抛物线与x轴的交点的知识,根据绝对值的性质把方程进行变形并解出方程是解题的关键.

练习册系列答案
相关题目
7.下列不等式变形正确的是( )
| A. | 若a>b,则a-2>b-2 | B. | 若$-\frac{1}{2}a<2$,则a<-4 | ||
| C. | 若a>b,则1-2a>1-2b | D. | 若a<b,则ac2<bc2 |
8. 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )
 如图所示几何体的主视图是( )
如图所示几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
4. 利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.
利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.
(1)如何搭建使矩形菜地的面积为200平方米?
(2)如何搭建使矩形菜地的面积最大,最大为多少平方米?
 利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.
利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.(1)如何搭建使矩形菜地的面积为200平方米?
(2)如何搭建使矩形菜地的面积最大,最大为多少平方米?
11.已知点A(a,1)与点B(5,b)关于点(3,2)对称,则a+b=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.若关于x的方程$\frac{x-2}{x+1}$=$\frac{m}{x+1}$产生增根,则常数m的值( )
| A. | -2 | B. | -1 | C. | -3 | D. | 2 |
8.据调查,2011年5月茶陵县的房价均价为2600元/m2,2013年同期将达到3200元/m2,假设这两年茶陵县房价的平均增长率为x,根据题意,所列方程为( )
| A. | 2600(1+x%)2=3200 | B. | 2600(1-x%)2=3200 | C. | 2600(1+x)2=3200 | D. | 2600(1+x)2=3200 |
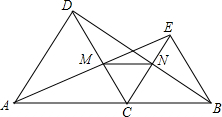 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下四个结论:①AE=BD;②CN=CM;③MN∥AB;④ME=NB.其中正确结论的个数是4.
如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下四个结论:①AE=BD;②CN=CM;③MN∥AB;④ME=NB.其中正确结论的个数是4.