题目内容
4. 利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.
利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地,菜地有2个2米宽的门,门用其它材料.(1)如何搭建使矩形菜地的面积为200平方米?
(2)如何搭建使矩形菜地的面积最大,最大为多少平方米?
分析 (1)设垂直于墙的篱笆长为x米,则平行于墙的长为:(50-3x)m,利用矩形面积求法得出答案;
(2)利用二次函数增减性得出x=$\frac{28}{3}$时,S最大,进而求出即可.
解答 解:(1)设垂直于墙的篱笆长为x米,则平行于墙的长为:(50-3x)m,
根据题意可得:x(50-3x)=200,
解得:x1=$\frac{20}{3}$,x2=10,
∵$\left\{\begin{array}{l}{x>0}\\{3x<46}\\{50-3x>0}\\{50-3x≤22}\end{array}\right.$,
解得:$\frac{28}{3}$≤x<$\frac{46}{3}$,
∴x=$\frac{20}{3}$(不合题意舍去),
答:垂直于墙的篱笆长为10米,平行于墙的长为20米;
(2)设总面积为:S平方米,根据题意可得:
S=x(50-3x)=-3x2+50x=-3(x-$\frac{25}{3}$)2+$\frac{625}{3}$,
∵$\frac{28}{3}$≤x<$\frac{46}{3}$,
∴x=$\frac{28}{3}$时,S最大为:205$\frac{1}{3}$平方米,
答:当宽度为$\frac{28}{3}$m,长度为22米,搭建使矩形菜地的面积最大,最大为205$\frac{1}{3}$平方米.
点评 此题主要考查了一元二次方程的应用以及二次函数的应用,根据二次函数增减性得出其最值是解题关键.

练习册系列答案
相关题目
16. 如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
 如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )
如图,在折纸活动中,李红制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿DE折叠压平,A与F重合,若∠A=70°,则∠1+∠2等于( )| A. | 70° | B. | 110° | C. | 130° | D. | 140° |
20. 某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图:
某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图:
(1)写出表中a,b,c的值;
(2)补全条形图;
(3)商场经理准备购进同一品牌的旅游鞋1500双,请根据市场实际情况估计他应该购进38码的鞋多少双?
 某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图:
某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图:| 尺码(码) | 数量(双) | 百分比(%) |
| 36 | 60 | 30 |
| 37 | 30 | 15 |
| 38 | a | b |
| 39 | 40 | 20 |
| 40 | c | 5 |
| 41 | 10 | 5 |
(2)补全条形图;
(3)商场经理准备购进同一品牌的旅游鞋1500双,请根据市场实际情况估计他应该购进38码的鞋多少双?
13.已知关于x的一元二次方程x2+(2m-3)x+m2=0的两个不相等的实数根α,β满足$\frac{1}{α}$+$\frac{1}{β}$=1,则m的值为( )
| A. | -3 | B. | 1 | C. | -3 或1 | D. | 2 |
14.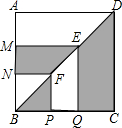 如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
 如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )| A. | $\frac{1}{4}$x2 | B. | $\frac{1}{2}$x2 | C. | $\frac{1}{5}$x2 | D. | $\frac{1}{3}$x2 |
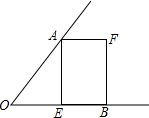 请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法)
请按要求,只用无刻度的直尺作图(请保留画图痕迹,不写作法)