题目内容
19.在矩形ABCD中,AB=4,BC=6,点M是AB的中点,点N是BC上的一动点,连接AN交DM,BD于点E、F.(1)若BN=NC,如图1,
①求证:FN=$\frac{1}{2}$AF;
②求EF;
(2)若BN=2NC,如图2,直接写出AE:EF:FN=15:9:16(不用说明理由)

分析 (1)①根据BN∥AD,得出△AFD∽△NFB,再根据相似三角形的对应边成比例,即可得到$\frac{FN}{FA}$=$\frac{1}{2}$,据此可得FN=$\frac{1}{2}$AF;
②下根据①中的结论得到AF=$\frac{2}{3}$AN=$\frac{10}{3}$,再延长DM交CB的延长线于G,根据△AED∽△NEG,求得AE=$\frac{2}{5}$AN=2,最后根据EF=AF-AE进行计算即可;
(2)先根据△AFD∽△NFB,求得FN=$\frac{2}{5}$AN,再延长DM交CB的延长线于G,根据△AED∽△NEG,求得AE=$\frac{3}{8}$AN,进而得到EF=AN-AE-FN=AN-$\frac{3}{8}$AN-$\frac{2}{5}$AN=$\frac{9}{40}$AN,最后根据AE:EF:FN=$\frac{3}{8}$:$\frac{9}{40}$:$\frac{2}{5}$进行化简即可.
解答 解:(1)①∵BN∥AD,
∴△AFD∽△NFB,
∴$\frac{FN}{FA}$=$\frac{BN}{DA}$,
∵BN=NC=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴$\frac{BN}{DA}$=$\frac{1}{2}$,即$\frac{FN}{FA}$=$\frac{1}{2}$,
∴FN=$\frac{1}{2}$AF;
②∵AB=4,BC=6,点M是AB的中点,
∴BN=3,AN=5,
∵$\frac{BN}{DA}$=$\frac{FN}{FA}$=$\frac{1}{2}$,
∴FN=$\frac{1}{2}$AF,即AF=$\frac{2}{3}$AN=$\frac{10}{3}$,
如图1,延长DM交CB的延长线于G,则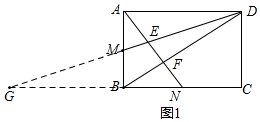
∵AD∥GB,
∴$\frac{AD}{BG}$=$\frac{AM}{BM}$=1,
∴AD=BG=2BN,即$\frac{AD}{GN}$=$\frac{2}{3}$,
∵AD∥GN,
∴△AED∽△NEG,
∴$\frac{AE}{NE}$=$\frac{AD}{NG}$=$\frac{2}{3}$,
∴AE=$\frac{2}{5}$AN=2,
∴EF=AF-AE=$\frac{10}{3}$-2=$\frac{4}{3}$;
(2)∵AD∥BN,
∴△AFD∽△NFB,
∴$\frac{FN}{FA}$=$\frac{BN}{DA}$,
又∵BN=2NC,
∴BN=$\frac{2}{3}$BC=4,而AD=6,
∴$\frac{FN}{FA}$=$\frac{2}{3}$,即FN=$\frac{2}{5}$AN,
如图2,延长DM交CB的延长线于G,则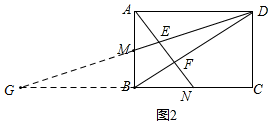
∵AD∥GB,
∴$\frac{AD}{BG}$=$\frac{AM}{BM}$=1,
∴AD=BG=6,GN=6+4=10,
∵AD∥GN,
∴△AED∽△NEG,
∴$\frac{AE}{NE}$=$\frac{AD}{NG}$=$\frac{3}{5}$,
∴AE=$\frac{3}{8}$AN,
∴EF=AN-AE-FN=AN-$\frac{3}{8}$AN-$\frac{2}{5}$AN=$\frac{9}{40}$AN,
∴AE:EF:FN=$\frac{3}{8}$:$\frac{9}{40}$:$\frac{2}{5}$=15:9:16.
故答案为:15:9:16.
点评 本题属于四边形综合题,主要考查了矩形的性质,相似三角形的判定与性质的运用,解决问题的关键是作辅助线构造相似三角形,依据相似三角形的对应边成比例进行求解.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案(1)函数y=$\frac{4}{(x-1)^{2}+1}$的自变量x的取值范围是全体实数;
(2)如表是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{5}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y=$\frac{4}{(x-1)^{2}+1}$的大致图象;

(4)结合函数图象,请写出函数y=$\frac{4}{(x-1)^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)解决问题:如果函数y=$\frac{4}{(x-1)^{2}+1}$与直线y=a的交点有2个,那么a的取值范围是0<a<4.
 如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,把△ADE绕点A旋转,旋转角为α(0°<α<180°),得到△AD'E'.
如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,把△ADE绕点A旋转,旋转角为α(0°<α<180°),得到△AD'E'. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章,记载了一道“折竹抵地”问题,叙述为:“今有竹高一丈,末折抵地,去本三尺,问折者几何?”翻译成数学问题是:在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,可列出的方程为x2+32=(10-x)2.
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章,记载了一道“折竹抵地”问题,叙述为:“今有竹高一丈,末折抵地,去本三尺,问折者几何?”翻译成数学问题是:在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,可列出的方程为x2+32=(10-x)2. 如图,点P在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过P作x轴,y轴的垂线,垂足分别为点A,B,已知矩形PAOB的面积为3,则k=-3.
如图,点P在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过P作x轴,y轴的垂线,垂足分别为点A,B,已知矩形PAOB的面积为3,则k=-3.