题目内容
7．
《九章算术》是我国古代最重要的数学著作之一，在“勾股”章，记载了一道“折竹抵地”问题，叙述为：“今有竹高一丈，末折抵地，去本三尺，问折者几何？”翻译成数学问题是：在Rt△ABC中，∠ACB=90°，AC+AB=10，BC=3，求AC的长，如果设AC=x，可列出的方程为x2+32=（10-x）2．
分析 设AC=x，可知AB=10-x，再根据勾股定理即可得出结论．
解答 解：设AC=x，
∵AC+AB=10，
∴AB=10-x．
∵在Rt△ABC中，∠ACB=90°，
∴AC2+BC2=AB2，即x2+32=（10-x）2．
故答案为：x2+32=（10-x）2．
点评 本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
练习册系列答案
相关题目
如图，在边长为2的菱形ABCD中，∠ABC=120°，E，F分别为AD，CD上的动点，且AE+CF=2，则线段EF长的最小值是$\sqrt{3}$．
2．
某校决定在4月7日开展“世界无烟日”宣传活动，活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式．学校围绕“你最喜欢的宣传方式是什么？”在全校学生中进行随机抽样调查（四个选项中必选且只选一项），根据调查统计结果，绘制了两种不完整的统计图表：
请结合统计图表，回答下列问题：
（1）本次抽查的学生共300人，m=30%，并将条形统计图补充完整；
（2）若该校学生有1500人，请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人？
（3）学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示，请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率．
某校决定在4月7日开展“世界无烟日”宣传活动，活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式．学校围绕“你最喜欢的宣传方式是什么？”在全校学生中进行随机抽样调查（四个选项中必选且只选一项），根据调查统计结果，绘制了两种不完整的统计图表：| 选项 | 方式 | 百分比 |
| A | 社区板报 | 35% |
| B | 集会演讲 | m |
| C | 喇叭广播 | 25% |
| D | 发宣传画 | 10% |
（1）本次抽查的学生共300人，m=30%，并将条形统计图补充完整；
（2）若该校学生有1500人，请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人？
（3）学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示，请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率．
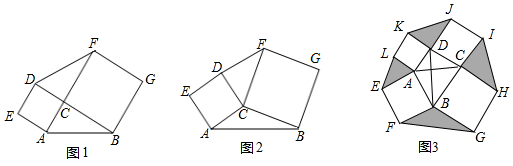
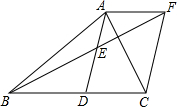已知：在△ABC中，AD是BC边上的中线，点E是AD的中点；过点A作AF∥BC，交BE的延长线于F，连接CF．
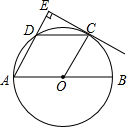如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E．