题目内容
8.(1)解方程:$\frac{1}{x-1}$=$\frac{3}{{x}^{2}-1}$(2)解不等式组:$\left\{\begin{array}{l}{x-2(x-3)<6}\\{x-1≤\frac{x+1}{3}}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答 解:(1)去分母得:x+1=3,
解得:x=2,
经检验x=2是分式方程的解;
(2)$\left\{\begin{array}{l}{x-2(x-3)<6①}\\{x-1≤\frac{x+1}{3}②}\end{array}\right.$,
由①得:x>0,
由②得:x≤2,
则不等式组的解集为0<x≤2.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.下列判断错误的是( )
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
 如图,在边长为2的菱形ABCD中,∠ABC=120°,E,F分别为AD,CD上的动点,且AE+CF=2,则线段EF长的最小值是$\sqrt{3}$.
如图,在边长为2的菱形ABCD中,∠ABC=120°,E,F分别为AD,CD上的动点,且AE+CF=2,则线段EF长的最小值是$\sqrt{3}$.
 图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):
图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):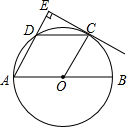 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.


