题目内容
9.已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的上边作正方形ADEF,连接CF.(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:BC⊥CF;②BC、CD、CF之间的数量关系为:CF=BC-CD.
(2)数学思考:如图2,当点D在线段CB的延长线上时,以上①②关系是否成立,请在后面的横线上写出正确的结论.①BC与CF的位置关系为:BC⊥CF;②BC、CD、CF之间的数量关系为:CF=CD-BC.
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若已知AB=2$\sqrt{2}$,CD=$\frac{1}{4}$BC,请求出DG的长(写出求解过程).

分析 (1)①证出∠BAD=∠CAF,由SAS证明△BAD≌△CAF,得出∠ACF=∠ABD=45°,证出∠ACF+∠ACB=90°,即可得出结论;
②由全等三角形的性质得出BD=CF,证出CF=BC-CD即可;
(2)①证出∠BAD=∠CAF,由SAS证明△BAD≌△CAF,得出∠ACF=∠ABD=180°-45°=135°,证出∠ACB+∠FCB=135°,得出∠FCB=90°,即可得出结论;
②由全等三角形的性质得出BD=CF,证出CF=CD-BC即可;
(3)由SAS证明△BAD≌△CAF,得出∠ACF=∠ABD=45°,证出∠FCB=∠ACF+∠ACB=90°,得出CF⊥BC,在Rt△ABC中,由勾股定理得出AC=AB=2$\sqrt{2}$,在Rt△AGC中,得出CG=$\sqrt{2}$AC=$\sqrt{2}$×2$\sqrt{2}$=4,同理BC=4,CD=$\frac{1}{4}$BC=1,在Rt△DCG中,由勾股定理即可求出DG的长.
解答 (1)证明:①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴∠BCF=90°,
∴BC⊥CF,
故答案为:BC⊥CF;
②由①△BAD≌△CAF,
∴BD=CF,
∵BD=BC-CD,
∴CF=BC-CD,
故答案为:CF=BC-CD;
(2)解:①成立,②不成立;理由如下:
①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAF+∠FAC=90°,∠DAF=∠BAF+∠DAB=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°,
∴∠ACB+∠FCB=135°,
∴∠FCB=90°,
∴BC⊥CF,
故答案为:BC⊥CF;
②由①△BAD≌△CAF,
∴BD=CF,
∵BD=CD-BC,
∴CF=CD-BC,
故答案为:CF=CD-BC;
(3)解:由题意得:∠BAC=∠FAD=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠FCB=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BC,
在Rt△ABC中,AC=AB=2$\sqrt{2}$,
在Rt△AGC中,∵∠ACF=45°,
∴CG=$\sqrt{2}$AC=$\sqrt{2}$×2$\sqrt{2}$=4,
同理BC=4,
CD=$\frac{1}{4}$BC=$\frac{1}{4}$×4=1,
∴在Rt△DCG中,DG=$\sqrt{C{G}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$.
点评 本题是四边形综合题目,主要考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识,熟练掌握全等三角形的判定与性质、等腰直角三角形的判定与性质是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,AB是⊙O的直径,点F、C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB是⊙O的直径,点F、C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2$\sqrt{3}$,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2 | D. | 4 |
| A. | 抛掷2枚正方体骰子,都是6点朝上 | |
| B. | 抛掷2枚硬币,朝上的都是反面 | |
| C. | 从只装有红球的袋子中摸出白球 | |
| D. | 从只装有红、篮球的袋子中摸出篮球 |

 图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):
图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):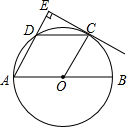 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E. 如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为11cm.
如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为11cm.



