题目内容
5．
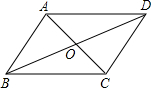如图，?ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（ ）| A． | 13 | B． | 17 | C． | 20 | D． | 26 |
分析 由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
解答 解：∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B．
点评 本题主要考查了平行四边形的性质，并利用性质解题．平行四边形基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．
练习册系列答案
相关题目
18．
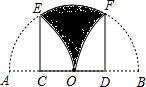如图，在以点O为圆心的半圆中，AB为直径，且AB=4，将该半圆折叠，使点A和点B落在点O处，折痕分别为EC和FD，则图中阴影部分面积为（ ）
如图，在以点O为圆心的半圆中，AB为直径，且AB=4，将该半圆折叠，使点A和点B落在点O处，折痕分别为EC和FD，则图中阴影部分面积为（ ）| A． | 4$\sqrt{3}$-$\frac{π}{3}$ | B． | 4$\sqrt{3}$-$\frac{2π}{3}$ | C． | 2$\sqrt{3}$-$\frac{π}{3}$ | D． | 2$\sqrt{3}$-$\frac{2π}{3}$ |
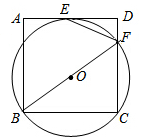如图，过正方形ABCD顶点B，C的⊙O与AD相切于点E，与CD相交于点F，连接EF．
我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，-4），连接AO，AO=5，sin∠AOC=$\frac{3}{5}$．
禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A、B两处距离为200海里，可疑船只正沿南偏东45°方向航行，我渔政船迅速沿北偏东30°方向前去拦截，经历4小时刚好在C处将可疑船只拦截．求该可疑船只航行的平均速度（结果保留根号）．