题目内容
2.已知m=$\sqrt{9-x}$,n=$\sqrt{72}$,p=$\sqrt{15}$.(1)当x=-1时,求(p+m)(p-m)+n的值;
(2)若m,n,p为Rt△ABC的三边长,求x的值.
分析 (1)首先把(p+m)(p-m)+n利用平方差化简,然后再代入m、n、p、x的值即可;
(2)此题要分两种情况:①当n为斜边时,②当m为斜边时,分别利用勾股定理计算出x的值.
解答 解:(1)(p+m)(p-m)+n=p2-m2+n,
∵m=$\sqrt{9-x}$,n=$\sqrt{72}$,p=$\sqrt{15}$,
∴原式=15-9+x+$\sqrt{72}$=5+6$\sqrt{2}$;
(2)当n为斜边时,($\sqrt{9-x}$)2+($\sqrt{15}$)2=($\sqrt{72}$)2,
解得:x=-48,
当m为斜边时,($\sqrt{9-x}$)2=($\sqrt{15}$)2+($\sqrt{72}$)2,
解得:x=-78.
点评 此题主要考查了二次根式的应用,以及勾股定理的应用,关键是掌握直角三角形两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目

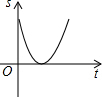
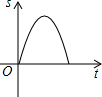
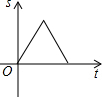
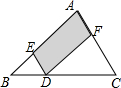 如图,在△ABC中,动点D从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动到点C(点D不与点B、C重合),运动时间为t,过点D作DE∥AC,DE∥AB,分别交AB于点E,交AC于点F,则图中阴影部分的面积S与时间t之间的函数图象大致为( )
如图,在△ABC中,动点D从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动到点C(点D不与点B、C重合),运动时间为t,过点D作DE∥AC,DE∥AB,分别交AB于点E,交AC于点F,则图中阴影部分的面积S与时间t之间的函数图象大致为( )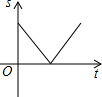
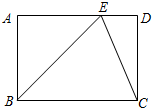 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.