题目内容
14.图1,图2均为正方形网络,每个小正方形的面积均为1.在这个正方形网格中,各个小正方形的顶点叫做格点.请在下面的网格中按要求画图,使得每个图形的顶点均在格点上.(1)在图1中,画一个边长为整数的矩形,面积等于24,周长等于22.
(2)在图2中,画一个有一个角是钝角的等腰三角形,且面积等于10.
分析 (1)根据长方形的面积、周长公式,画一个长和宽为8和3的长方形即可;
(2)根据勾股定理确定出三角形的腰长,再由钝角三角形的性质画出图形即可.
解答 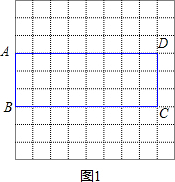 解:(1)设该长方形的长为a,宽为b,则
解:(1)设该长方形的长为a,宽为b,则
a+b=11,ab=24,
显然a、b是关于x的一元二次方程x2-11x+28=0的两根,
解方程x2-11x+28=0得到x1=8,x2=3,
即a=8,b=3,
所以该矩形的长为8,宽为3,如图1所示的矩形ABCD.
(2)如图2所示,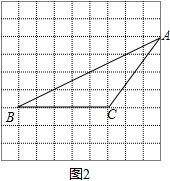 AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=5,
AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=5,
S△ABC=$\frac{1}{2}$×4×5=10.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.下列选项中,是方程x-2y=10的解是( )
| A. | $\left\{\begin{array}{l}x=2\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-2\\ y=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-2\\ y=-4\end{array}\right.$ |
6.三位老师周末到某家电专卖店购买冰箱和空调,正值该专卖店举行“迎新春、大优惠”活动,具体优惠情况如下表:
(1)李老师所购物品的原价是6000元,李老师实际付5000元
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
| 购物总金额(原价) | 折扣率 |
| 不超过3000元的部分 | 九折 |
| 超过3000元但不超过5000元的部分 | 八折 |
| 超过5000元的部分 | 七折 |
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
4.下列数:-3,1,-2,0中,最小的是( )
| A. | -3 | B. | 0 | C. | -2 | D. | 1 |
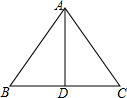 如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.
如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.