题目内容
11.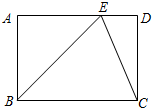 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.(1)△BEC是否为等腰三角形?为什么?
(2)若AB=a,∠ABE=45°,求BC的长.
分析 (1)求出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=a,根据勾股定理求出BE即可.
解答 解:(1)△BEC是等腰三角形,理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵EC平分∠DEB,
∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,
即△BEC是等腰三角形.
(2)∵四边形ABCD是矩形,
∴∠A=90°,
∵∠ABE=45°,
∴∠ABE=AEB=45°,
∴AB=AE=a,
由勾股定理得:BE=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a,
即BC=BE=$\sqrt{2}$a.
点评 本题考查了矩形的性质、等腰三角形的判定与性质、勾股定理的应用等知识;熟练掌握矩形的性质、等腰三角形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列选项中,是方程x-2y=10的解是( )
| A. | $\left\{\begin{array}{l}x=2\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-2\\ y=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-2\\ y=-4\end{array}\right.$ |
6.三位老师周末到某家电专卖店购买冰箱和空调,正值该专卖店举行“迎新春、大优惠”活动,具体优惠情况如下表:
(1)李老师所购物品的原价是6000元,李老师实际付5000元
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
| 购物总金额(原价) | 折扣率 |
| 不超过3000元的部分 | 九折 |
| 超过3000元但不超过5000元的部分 | 八折 |
| 超过5000元的部分 | 七折 |
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
 如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度.
如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度.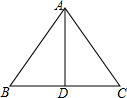 如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.
如图,在△ABC中,AB=10,BC=12,AD是BC边上的中线且AD=8.求证:△ABC是等腰三角形.