题目内容
6.(1)先化简,再求值.($\frac{2}{x-1}$+$\frac{1}{x+1}$)•(x2-1),其中x=$\frac{\sqrt{3}-1}{3}$.(2)计算:|4-$\sqrt{17}$|-($\frac{\sqrt{34}}{2}$-$\sqrt{8}$)×$\sqrt{2}$+($\frac{1}{3}$)-1.
分析 (1)首先对括号内的分式通分相加,然后转化为乘法计算,即可化简,然后代入数值计算即可;
(2)首先去掉绝对值符号,计算二次根式的乘法和负指数次幂,然后合并同类二次根式即可.
解答 解:(1)原式=$\frac{2(x+1)+(x-1)}{(x+1)(x-1)}$•(x+1)(x-1)
=2x+2+x-1
=3x+1,
当x=$\frac{\sqrt{3}-1}{3}$时,原式=$\sqrt{3}$;
(2)原式=$\sqrt{17}$-4-($\sqrt{17}$-4)+3
=3.
点评 本题考查了分式的化简求值,正确对分式进行通分、约分变形,正确进行分解因式是关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
1.如果把分式$\frac{x-y}{x+y}$中的x和y都扩大原来的2倍,则分式的值( )
| A. | 扩大4倍 | B. | 扩大2倍 | C. | 不变 | D. | 缩小2倍 |
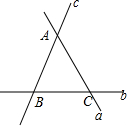 如图,直线a,b,c两两相交于A,B,C三点,则图中有6对对顶角;有12对同位角;有6对内错角;有6对同旁内角.
如图,直线a,b,c两两相交于A,B,C三点,则图中有6对对顶角;有12对同位角;有6对内错角;有6对同旁内角.
 在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.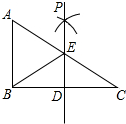 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )