题目内容

11．（1）解方程x2-2x-3=0
（2）解不等式组$\left\{\begin{array}{l}{2-x＞0}\\{\frac{5x+1}{2}≥x}\end{array}\right.$．

分析 （1）利用因式分解法解方程；
（2）分别解两个不等式得到x＜2和x≥-1，然后根据大于小的小于大的取中间确定不等式组的解集．

解答 解：（1）（x-3）（x+1）=0，
x-3=0或x+1=0，
所以x1=3，x2=-1；
（2）$\left\{\begin{array}{l}{2-x＞0①}\\{\frac{5x+1}{2}≥x②}\end{array}\right.$，
解①得x＜2，
解②得x≥-1，
所以不等式组的解集为-1≤x＜2．

点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了解一元一次不等式组．

练习册系列答案
相关题目
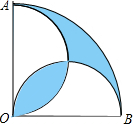1．如图，在圆心角为直角的扇形OAB中，分别以OA、OB为直径作两个半圆，向直角扇形OAB内随机取一点，则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$．
2．如图，长方形OABC在平面直角坐标系内（O为坐标原点），点A在x轴上，点C在y轴上，点B的坐标为（-2，2$\sqrt{3}$），点E是BC的中点，点H在OA上，且AH=$\frac{1}{2}$，过点H且平行于y轴的HG与EB交于点G，现将长方形折叠，使顶点C落在HG上，并与HG上的点D重合，折痕为EF，且折痕交y轴于点F．试求：
（1）∠CEF的度数和点D的坐标；
（2）折痕EF所在直线的函数解析式；
（3）在y轴上是否存在点M使得S△EFD=S△EFM？若存在，求出点M的坐标，若不存在，请说明理由；
（4）若点P在直线EF上，当△PFD为等腰三角形时，试问满足条件的点P有几个，请求出点P的坐标（不必写出解答过程）．
19．若关于x的不等式组$\left\{\begin{array}{l}{a-\frac{x}{4}＞0，①}\\{x＞3a+5②}\end{array}\right.$无解，求a的取值范围．
6．（1）先化简，再求值．（$\frac{2}{x-1}$+$\frac{1}{x+1}$）•（x2-1），其中x=$\frac{\sqrt{3}-1}{3}$．
（2）计算：|4-$\sqrt{17}$|-（$\frac{\sqrt{34}}{2}$-$\sqrt{8}$）×$\sqrt{2}$+（$\frac{1}{3}$）-1．
16．先化简（$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$-$\frac{x}{x+2}$）÷$\frac{x-1}{x+2}$，再选取一个你喜欢的数代入求值．
3．先化简，再求值：$\frac{x-1}{x}÷\frac{{x}^{2}-1}{{x}^{2}+2x}-1$，其中x=|2-$\sqrt{3}$|+2sin60°．
20．2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年，9月3日全国各地举行有关纪念活动，为了解初中学生对二战历史的知晓情况，某初中课外兴趣小组在本校学生中开展了专题调查活动，随机抽取了部分学生进行问卷调查，根据学生的答题情况，将结果分为A，B，C，D四类，其中A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”；D类表示“不太了解”，调查的数据经整理后形成尚未完成的条形统计图（如图①）和扇形统计图（如图②）：

（1）在这次抽样调查中，一共抽查了200名学生；
（2）请把图①中的条形统计图补充完整；
（3）图②的扇形统计图中D类部分所对应扇形的圆心角的度数为36°；
（4）如果这所学校共有初中学生1500名，请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名？
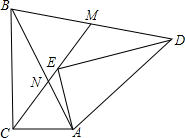6．如图，Rt△ABC中，∠BCA=90°，∠BAC=α，将△ABC旋转一个角度后得到△AED，CE交AB于点N，交BD于点M．
（1）求证：M为BD的中点；
（2）若CN=CA=m，求BD的长（用含m、n的式子表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网