题目内容
9．
如图，直线l∥m∥n，等边△ABC的顶点B，C分别在直线n和m上，边BC与直线n所夹的角为25°，则∠α的度数为35度．
分析 先根据m∥n求出∠BCD的度数，再由△ABC是等边三角形求出∠ACB的度数，根据l∥m即可得出结论．
解答 
解：∵m∥n，边BC与直线n所夹的角为25°，
∴∠BCD=25°．
∵△ABC是等边三角形，
∴∠ACB=60°，
∴∠ACD=60°-25°=35°．
∵l∥m，
∴∠α=∠ACD=35°．
故答案为：35．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
相关题目
19．与-2的和为0的数是（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
17．
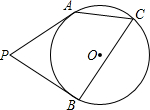如图，PA、PB与⊙O相切于A、B两点，C为优弧$\widehat{AB}$上一点，若tan∠ACB=2，则sin∠APB的值为（ ）
如图，PA、PB与⊙O相切于A、B两点，C为优弧$\widehat{AB}$上一点，若tan∠ACB=2，则sin∠APB的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{12}$ | D． | $\frac{\sqrt{5}}{5}$ |
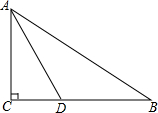如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于点D．