题目内容
15. 已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).
已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).(1)求证:该方程有两个不相等的实数根;
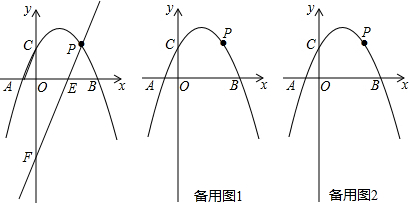
(2)当抛物线y=-x2+(m+1)x+(m+2)经过点(3,0),求该抛物线的表达式;
(3)在(2)的条件下,记抛物线y=-x2+(m+1)x+(m+2)在第一象限之间的部分为图象G,如果直线y=k(x+1)+4与图象G有公共点,请结合函数的图象,求直线y=k(x+1)+4与y轴交点的纵坐标t的取值范围.
分析 (1)利用根的判别式的符号进行证明;
(2)把点(3,0)代入函数解析式,列出关于m的方程,通过解方程来求m的值;
(3)根据函数解析式y=-x2+2x+3求得抛物线的顶点坐标,当直线y=k(x+1)+4经过顶点(1,4)时,此时直线y=k(x+1)+4与y轴交点的纵坐标为4.
当x=0时,y=3,此时直线y=k(x+1)+4与y轴交点的纵坐标为3.结合函数图象可知,3<t≤4.
解答 (1)证明:∵△=(m+1)2-4×(-1)×(m+2)
=(m+3)2.
∵m>0,
∴(m+3)2>0,
即△>0,
∴原方程有两个不相等的实数根;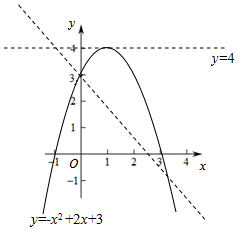 (2)解:∵抛物线抛物线y=-x2+(m+1)x+(m+2)经过点(3,0),
(2)解:∵抛物线抛物线y=-x2+(m+1)x+(m+2)经过点(3,0),
∴-32+3(m+1)+(m+2)=0,
∴m=1.
∴y=-x2+2x+3.
(3)解:∵y=-x2+2x+3=-(x-1)2+4,
∴该抛物线的顶点为(1,4).
∴当直线y=k(x+1)+4经过顶点(1,4)时,
∴4=k(1+1)+4,
∴k=0,
∴y=4.
∴此时直线y=k(x+1)+4与y轴交点的纵坐标为4.
∵y=-x2+2x+3,
∴当x=0时,y=3,
∴该抛物线与y轴的交点为(0,3).
∴此时直线y=k(x+1)+4与y轴交点的纵坐标为3.
∴3<t≤4.
点评 本题考查了待定系数法求解析式,根的判别式,二次函数图象与几何变换.
总结:利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
上面的结论反过来也成立.

练习册系列答案
相关题目
5.下列代数式中是二次二项式的是( )
| A. | xy-1 | B. | $\frac{1}{{x}^{2}+1}$ | C. | x2+xy2 | D. | $\sqrt{{x}^{4}+1}$ |
6.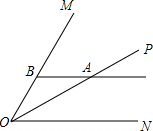 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
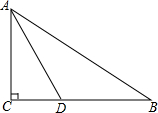 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.