题目内容
12．一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，则k的取值范围是（ ）| A． | k＜2且k≠1 | B． | k＞2且k≠1 | C． | k＞2 | D． | k＜2 |
分析 根据题意可得△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，求出k的取值范围即可．
解答 解：∵一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，
∴△=b2-4ac=4-4（1-k）×（-1）＞0，且1-k≠0，
解得：k＜2，且k≠1．
故选A．
点评 此题主要考查了一元二次方程根的情况与判别式，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
2．
如图，∠ABC=50°，AD垂直平分线段BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是（ ）
如图，∠ABC=50°，AD垂直平分线段BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是（ ）| A． | 115° | B． | 75° | C． | 105° | D． | 50° |
17．
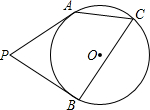如图，PA、PB与⊙O相切于A、B两点，C为优弧$\widehat{AB}$上一点，若tan∠ACB=2，则sin∠APB的值为（ ）
如图，PA、PB与⊙O相切于A、B两点，C为优弧$\widehat{AB}$上一点，若tan∠ACB=2，则sin∠APB的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{12}$ | D． | $\frac{\sqrt{5}}{5}$ |
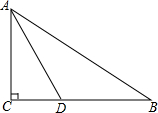如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于点D．