题目内容
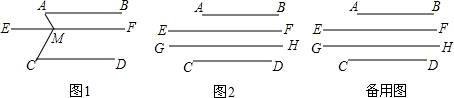
 如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.
如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.考点:平行线的判定与性质
专题:证明题
分析:求出∠EDC=
∠ADC,∠ABF=
∠ABC,推出∠EDC=∠ABF,求出∠AED=∠EDC,根据平行线的判定推出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:AB∥CD,
理由:∵DE、BF分别为∠ADC、∠ABC的平分线,∠ADC=∠ABC,
∴∠EDC=
∠ADC,∠ABF=
∠ABC,
∵∠ADC=∠ABC,
∴∠EDC=∠ABF,
∵∠AED=∠ABF,
∴∠AED=∠EDC,
∴AB∥CD.
理由:∵DE、BF分别为∠ADC、∠ABC的平分线,∠ADC=∠ABC,
∴∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC=∠ABC,
∴∠EDC=∠ABF,
∵∠AED=∠ABF,
∴∠AED=∠EDC,
∴AB∥CD.
点评:本题考查了对平行线的判定定理的应用,注意:平行线的判定定理有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
某商品连续两次9折降价销售,降价后每件商品的售价为a元,该产品原价为( )
| A、0.92a元 | ||
| B、1.12a元 | ||
C、
| ||
D、
|
一个样本有10个数据,各数据与样本平均数的差依次为:-4,-2,5,4,-1,0,2,3,-2,-5,那么这个样本的极差和方差分别是( )
| A、10,10 |
| B、10,10.4 |
| C、10.4,10.4 |
| D、0,10.4 |