题目内容
19.(1)计算:($\sqrt{2}$+$\sqrt{3}$)($\sqrt{2}$-$\sqrt{3}$)+2$\sqrt{12}$;(2)计算:|-3|+($\root{3}{27}$-1)0-$\sqrt{16}$+($\frac{1}{3}$)-1;
(3)解方程组:$\left\{\begin{array}{l}{4x-3y=11}\\{2x+y=13}\end{array}\right.$;
(4)解不等式组:$\left\{\begin{array}{l}{x+2≥0}\\{\frac{3x-1}{2}<\frac{2x+1}{3}}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)原式利用平方差公式计算,合并即可得到结果;
(2)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及算术平方根定义计算即可得到结果;
(3)方程组利用加减消元法求出解即可;
(4)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,表示在数轴上即可.
解答 解:(1)原式=2-3+4$\sqrt{3}$=4$\sqrt{3}$-1;
(2)原式=3+1-4+3=3;
(3)$\left\{\begin{array}{l}{4x-3y=11①}\\{2x+y=13②}\end{array}\right.$,
①+②×3得:10x=50,即x=5,
把x=5代入②得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{x+2≥0①}\\{\frac{3x-1}{2}<\frac{2x+1}{3}②}\end{array}\right.$,
由①得:x≥-2,
由②得:x<1,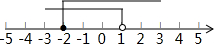
则不等式组的解集为-2≤x<1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
9.在今年的“希望工程”捐款活动中,某班级一小组7名同学积极捐出自己的零花锇,奉献自己的爱心,他们捐款的数额分别是(单位:元)5O、20、5O、30、25、50、55,这组数据的众数和中位数分别是( )
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
10.观察下列一组图形中黑点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第16个图中共有点的个数是( )
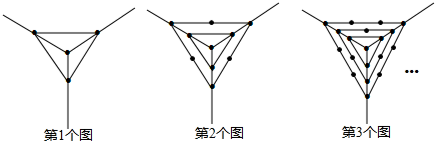

| A. | 408 | B. | 409 | C. | 361 | D. | 360 |
7. 如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
 如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )| A. | 8 | B. | 4 | C. | 5 | D. | 10 |
14.若关于x的一元二次方程(a+1)x2+x-a2+1=0有一个根为0,则a的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1或者-1 |
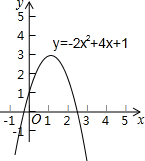 在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )