题目内容
 如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;
如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;(1)求抛物线的解析式;
(2)若抛物线的顶点为D,对称轴交x轴于点E,连接AD,点F为AD的中点,求出线段EF的长;
(3)若点P是抛物线上异于A、C的另外一点,且S△AEP=S△AED,求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)由于抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,根据待定系数法可求抛物线的解析式;
(2)先配方得到点D(1,-4),依此可得AE=2,ED=4,根据勾股定理可求AD,再根据直角三角形的性质可求线段EF的长;
(3)当点P的纵坐标是4时,S△AEP=S△AED,依此可得方程求出点P的纵坐标,从而求解.
(2)先配方得到点D(1,-4),依此可得AE=2,ED=4,根据勾股定理可求AD,再根据直角三角形的性质可求线段EF的长;
(3)当点P的纵坐标是4时,S△AEP=S△AED,依此可得方程求出点P的纵坐标,从而求解.
解答:解:(1)将A(-1,0),B(4,5)代入y=x2+bx+c得,
,
解得:
.
所以抛物线的解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
所以点D(1,-4),
所以AE=2,ED=4,AD=
=2
因为F是AD的中点,
所以EF=
AD=
;
(3)当点P的纵坐标是4时,S△AEP=S△AED,
则(x-1)2-4=4,
解得x=1±2
.
所以点P的坐标是(1+
,4)或(1-
,4).
|
解得:
|
所以抛物线的解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
所以点D(1,-4),
所以AE=2,ED=4,AD=
| AE2+ED2 |
| 5 |
因为F是AD的中点,
所以EF=
| 1 |
| 2 |
| 5 |
(3)当点P的纵坐标是4时,S△AEP=S△AED,
则(x-1)2-4=4,
解得x=1±2
| 2 |
所以点P的坐标是(1+
| 2 |
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,配方法,勾股定理,直角三角形的性质,三角形的面积,方程思想的应用,综合性较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,海岸线MN上有A,B两艘船,均收到已触角搁浅的船P求救信号.经测量,∠PAB=37°,∠PBA=67°,AB的距离为42海里.
如图,海岸线MN上有A,B两艘船,均收到已触角搁浅的船P求救信号.经测量,∠PAB=37°,∠PBA=67°,AB的距离为42海里.
 2013年12月23日,中央办公厅印发《关于培育和践行社会主义核心价值观的意见》,将社会主义24字核心价值观分成3个层面:富强、民主、文明、和谐,是国家层面的价值目标;自由、平等、公正、法治,是社会层面的价值取向;爱国、敬业、诚信、友善,是公民个人层面的价值准则.某校九年级(一)班的数学兴趣小组就“你了解社会主义核心价值观吗?”随机调查了本校部分同学,并对调查结果进行整理,绘制成如图尚不完整的统计图表:
2013年12月23日,中央办公厅印发《关于培育和践行社会主义核心价值观的意见》,将社会主义24字核心价值观分成3个层面:富强、民主、文明、和谐,是国家层面的价值目标;自由、平等、公正、法治,是社会层面的价值取向;爱国、敬业、诚信、友善,是公民个人层面的价值准则.某校九年级(一)班的数学兴趣小组就“你了解社会主义核心价值观吗?”随机调查了本校部分同学,并对调查结果进行整理,绘制成如图尚不完整的统计图表:
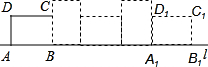 矩形ABCD的边AB=4,AD=3,现将矩形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当它翻滚至类似开始的位置时A1B1C1D1(如图所示),则顶点D所经过的路线长是
矩形ABCD的边AB=4,AD=3,现将矩形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当它翻滚至类似开始的位置时A1B1C1D1(如图所示),则顶点D所经过的路线长是