题目内容
如图,抛物线经过点A(1,0),B(5,0),C(0,
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.

(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
| 10 |
| 3 |

(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:几何综合题,压轴题
分析:(1)由抛物线经过点A(1,0),B(5,0),C(0,
)三点,利用待定系数法求二次函数的解析式;
(2)由点E(x,y)是抛物线上一动点,且位于第四象限,可得y<0,即-y>0,-y表示点E到OA的距离,又由S=2S△OBE=2×
×OB•|y|,即可求得平行四边形OEAF的面积S与x之间的函数关系式,结合图象,求得自变量x的取值范围;
(3)由当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,可得此时点E坐标只能(2.5,-2.5),而坐标为(2.5,-2.5)点在抛物线上,故可判定存在点E,使平行四边形OEBF为正方形.
| 10 |
| 3 |
(2)由点E(x,y)是抛物线上一动点,且位于第四象限,可得y<0,即-y>0,-y表示点E到OA的距离,又由S=2S△OBE=2×
| 1 |
| 2 |
(3)由当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,可得此时点E坐标只能(2.5,-2.5),而坐标为(2.5,-2.5)点在抛物线上,故可判定存在点E,使平行四边形OEBF为正方形.
解答:解:(1)设所求抛物线的解析式为y=ax2+bx+c,
∵抛物线经过点A(1,0),B(5,0),C(0,
)三点,则由题意可得:
,解得
.
∴所求抛物线的解析式为:y=
x2-4x+
.
(2)∵点E(x,y)是抛物线上一动点,且在x轴下方,
∴y<0,
即-y>0,-y表示点E到OA的距离.
∵OB是平行四边形OEBF的对角线,
∴S=2S△OBE=2×
×OB•|y|=-5y=-5(
x2-4x+
)=-
x2+20x-
,
∵S=-
(x-3)2+
∴S与x之间的函数关系式为:S=-
x2+20x-
(1<x<5),S的最大值为
.
(3)∵当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,
∴此时点E坐标只能(
,-
),而坐标为(
,-
)点在抛物线上,
∴存在点E(
,-
),使平行四边形OEBF为正方形,
此时点F坐标为(
,
).
∵抛物线经过点A(1,0),B(5,0),C(0,
| 10 |
| 3 |
|
|
∴所求抛物线的解析式为:y=
| 2 |
| 3 |
| 10 |
| 3 |
(2)∵点E(x,y)是抛物线上一动点,且在x轴下方,
∴y<0,
即-y>0,-y表示点E到OA的距离.
∵OB是平行四边形OEBF的对角线,
∴S=2S△OBE=2×
| 1 |
| 2 |
| 2 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
| 50 |
| 3 |
∵S=-
| 10 |
| 3 |
| 40 |
| 3 |
∴S与x之间的函数关系式为:S=-
| 10 |
| 3 |
| 50 |
| 3 |
| 40 |
| 3 |
(3)∵当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,
∴此时点E坐标只能(
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴存在点E(
| 5 |
| 2 |
| 5 |
| 2 |
此时点F坐标为(
| 5 |
| 2 |
| 5 |
| 2 |
点评:此题属于二次函数综合题,考查了待定系数法求二次函数的解析式、配方法、平行四边形的性质以及正方形的判定等知识.此题综合性很强,难度较大,注意数形结合思想、方程思想与函数思想的应用.

练习册系列答案
相关题目

 顶点为(-
顶点为(-

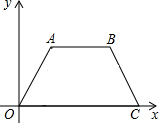 如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO=
如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO= 如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;
如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;