题目内容
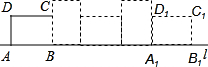矩形ABCD的边AB=4，AD=3，现将矩形ABCD放在直线l上且沿着l向右做无滑动地翻滚，当它翻滚至类似开始的位置时A1B1C1D1（如图所示），则顶点D所经过的路线长是考点：弧长的计算,旋转的性质
专题：
分析：根据图形的滚动路线得出顶点D所经过的路线长为3段扇形弧长进而求出即可．
解答：
解：连接BD．
在直角△ABD中，BD=
=
=5，
则顶点D所经过的路线长：
+
+
=6π．
故答案是：6π．
解：连接BD．在直角△ABD中，BD=
| AB2+AD2 |
| 32+42 |
则顶点D所经过的路线长：
| 90π×5 |
| 180 |
| 90π×4 |
| 180 |
| 90π×3 |
| 180 |
故答案是：6π．
点评：此题主要考查了图形的旋转以及扇形弧长公式和扇形面积公式应用，根据已知得出滚动路线是解题关键．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
如图，抛物线y=x2+bx+c经过A（-1，0），B（4，5）两点，请解答下列问题；
如图，在矩形纸片ABCD中，AB=4，AD=3，折叠纸片使DA与对角线DB重合，点A落在点A′处，折痕为DE，则A′E的长是
把一块直尺与一块三角板如图放置，若∠1=30°，则∠2的度数为在平面直角坐标系中，点A和点B关于原点对称，已知点A的坐标为（2，3），那么点B的坐标为（ ）
| A、（3，-2） |
| B、（2，-3） |
| C、（-3，2） |
| D、（-2，-3） |
如图，菱形花坛ABCD的边长为20m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD．求：