题目内容
已知抛物线y=-x2+2x+3.
(1)用配方法求它的顶点坐标和对称轴;
(2)直接写出抛物线与x轴的两个交点A、B(点A在点B的左侧)及与y轴的交点C的坐标.
(1)用配方法求它的顶点坐标和对称轴;
(2)直接写出抛物线与x轴的两个交点A、B(点A在点B的左侧)及与y轴的交点C的坐标.
考点:二次函数的三种形式,抛物线与x轴的交点
专题:
分析:(1)利用配方法把抛物线解析式配成顶点式y=-(x-1)2+4,然后根据二次函数的性质写出顶点坐标和对称轴;
(2)令y=0,解方程-x2+2x+3=0可得到A点和B点坐标;令x=0,则y=3,则可确定C点坐标.
(2)令y=0,解方程-x2+2x+3=0可得到A点和B点坐标;令x=0,则y=3,则可确定C点坐标.
解答:解:(1)∵y=-(x2-2x+1-1)+3=-(x-1)2+4,
∴抛物线的顶点坐标为(1,4),对称轴为直线x=1;
(2)∵y=-x2+2x+3,
∴当y=0时,-x2+2x+3=0,
解得x=-1或3,
∴A点坐标为(-1,0),B点坐标为(3,0);
∵x=0时,y=3,
∴C点坐标为(0,3).
∴抛物线的顶点坐标为(1,4),对称轴为直线x=1;
(2)∵y=-x2+2x+3,
∴当y=0时,-x2+2x+3=0,
解得x=-1或3,
∴A点坐标为(-1,0),B点坐标为(3,0);
∵x=0时,y=3,
∴C点坐标为(0,3).
点评:本题考查了二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).同时考查了抛物线与坐标轴的交点求法.

练习册系列答案
相关题目
今年23号台风“菲特”给宁波市生产生活带来严重影响,直接经济损失达333.6亿元,用科学记数法表示
“333.6亿元”为( )
“333.6亿元”为( )
| A、0.3336×1010元 |
| B、3.336×1010元 |
| C、0.3336×1011元 |
| D、3.336×1011元 |

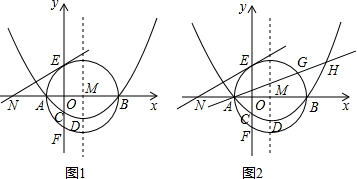
 顶点为(-
顶点为(- 如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;
如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题;