题目内容
18. 如图,AB是⊙O的直径,CD是弦,CD⊥AB于M,若AM•MB=4,求CD的长.
如图,AB是⊙O的直径,CD是弦,CD⊥AB于M,若AM•MB=4,求CD的长.
分析 连接AC,BC,根据圆周角定理得出∠ACB=90°,再由CD⊥AB可得出CM=DM,由相似三角形的判定定理得出△ACM∽△CBM,进而可得出结论.
解答  解:连接AC,BC,
解:连接AC,BC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵CD⊥AB,
∴CM=DM.
∵∠A+∠B=90°,∠A+∠ACM=90°,
∴∠ACM=∠B,∠AMC=∠CMB=90°,
∴△ACM∽△CBM,
∴$\frac{AM}{CM}$=$\frac{CM}{BM}$,即CM2=AM•BM=4,
∴CM=2,
∴CD=2CM=4.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | “a是任意实数,则a2≥0”是随机事件 | |
| B. | 某彩票的中奖率为1%,则买100张彩票一定有1张会中奖 | |
| C. | 若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为$\frac{1}{2}$ | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
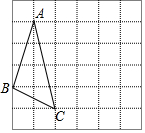 如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.
如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′. 如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度.
如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度. 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC. 如图,已知BA=BD,BC=BE,∠1=∠2,求证:AC=DE.
如图,已知BA=BD,BC=BE,∠1=∠2,求证:AC=DE. 一次函数y=kx+b的图象如图所示,求k与b的值.
一次函数y=kx+b的图象如图所示,求k与b的值.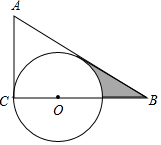 已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.
已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.