题目内容
6. 如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度.
如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度.
分析 先构造直角三角形,求出∠BEA=60°,进而用圆内接四边形的性质即可得出.
解答 解:如图,
作EH⊥BC,FG⊥BC,
∴HG=$\frac{1}{2}$BC,
∴HG=$\frac{1}{2}$EF,
作FM⊥EH,
∴FM=HG=$\frac{1}{2}$EF,
∴∠MEF=30°,
∴∠BEA=60°,
作内接四边形ADBN,
∴∠ADC=∠N,
∵∠N=$\frac{1}{2}$∠BEA=30°,
∴∠ADC=30°.
故答案为30
点评 此题是三角形内接圆与内心,主要考查了直角三角形性质,圆内接四边形的性质,解本题的关键是作出辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若a2n=3,则2a6n-1的值为( )
| A. | 17 | B. | 53 | C. | 35 | D. | 1457 |
1.计算:1÷(-5)×(-$\frac{1}{5}$)的结果是( )
| A. | 1 | B. | -1 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
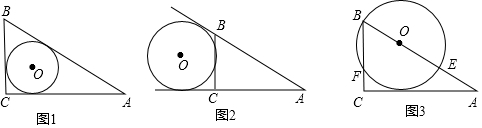
 如图,AB是⊙O的直径,CD是弦,CD⊥AB于M,若AM•MB=4,求CD的长.
如图,AB是⊙O的直径,CD是弦,CD⊥AB于M,若AM•MB=4,求CD的长.