题目内容
18.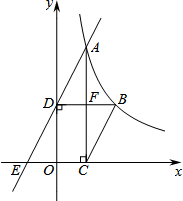 如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.
如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.(1)若AC=2OD时,
①直接写出点A坐标(1,4),四边形ADCB是菱形
②求a、b的值;
(2)若EC=3DB,求a的值.
分析 (1)①由函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2),可求得反比例函数的解析式,又由AC=2OD,可求得点A的纵坐标,则可求得点A坐标;由AF=CF=2,DF=BF=1,AC⊥BD,可证得四边形ADCB是菱形;
②将A与D的坐标代入,利用待定系数法即可求得a、b的值;
(2)首先设点C的坐标为(m,0),首先由EC=3DB,求得点E与点A的坐标,然后利用待定系数法即可求得一次函数的解析式.
解答 解:(1)∵函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2),
∴k=xy=2×2=4,OD=2,
∴反比例函数的解析式为:y=$\frac{4}{x}$,
①∵BD⊥y轴,
∴点D的坐标为:(0,2),即OD=2,
∵AC=2OD=2×2=4,AC⊥x轴,
∴点A的纵坐标为4,
∴4=$\frac{4}{x}$,
解得:x=1,
∴点A坐标为:(1,4);
∴AF=CF=2,DF=BF=1,
∴四边形ADCB是平行四边形,
∵AC⊥BD,
∴四边形ADCB是菱形;
故答案为:(1,4),菱;
②把点D与点A代入得:$\left\{\begin{array}{l}{b=2}\\{a+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$
∴a=2,b=2;
(2)∵EC=3DB,DB=2,
∴EC=6,
设点C的坐标为(m,0),则点A的坐标为:(m,$\frac{4}{m}$),
点E的坐标为:(m-6,0),
∵点D的坐标为(0,2),
∴b=2,
把E,A的坐标代入y=ax+2得:$\left\{\begin{array}{l}{am+2=\frac{4}{m}}&{①}\\{a(m-6)+2=0}&{②}\end{array}\right.$,
由②得a=$\frac{2}{6-m}$代入①,
得到$\frac{2m}{6-m}$+2=$\frac{4}{m}$,
解得m=$\frac{3}{2}$代入①可得a=$\frac{4}{9}$.
点评 此题属于反比例函数综合题.考查了待定系数求函数解析式以及菱形的判定的知识.注意求得各点的坐标是解此题的关键.

 名校课堂系列答案
名校课堂系列答案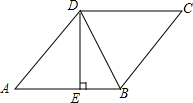 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | 10$\sqrt{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
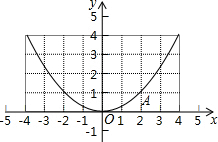 如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),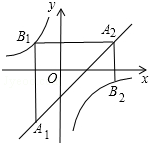 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.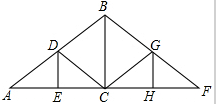 如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8m,则立柱BC,DE要多长?
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8m,则立柱BC,DE要多长?