题目内容
3.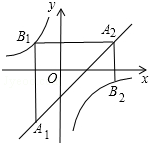 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
分析 首先根据a1=-1,求出a2=2,a3=$\frac{1}{2}$,a4=-1,a5=2,…,所以a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$;然后用2015除以3,根据商和余数的情况,判断出a2016是第几个循环的第几个数,进而求出它的值是多少即可.
解答 解:∵a1=-1,
∴B1的坐标是(-1,1),
∴A2的坐标是(2,1),
即a2=2,
∵a2=2,
∴B2的坐标是(2,-$\frac{1}{2}$),
∴A3的坐标是($\frac{1}{2}$,-$\frac{1}{2}$),
即a3=$\frac{1}{2}$,
∵a3=$\frac{1}{2}$,
∴B3的坐标是($\frac{1}{2}$,-2),
∴A4的坐标是(-1,-2),
即a4=-1,
∵a4=-1,
∴B4的坐标是(-1,1),
∴A5的坐标是(2,1),
即a5=2,
…,
∴a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$,
∵2016÷3=672,
∴a2016是第672个循环的第3个数,
∴a2016=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 (1)此题主要考查了反比例函数图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
(2)此题还考查了一次函数图象上的点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

 步步高达标卷系列答案
步步高达标卷系列答案| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
| A. | -2 | B. | 2 | C. | 4 | D. | -5 |
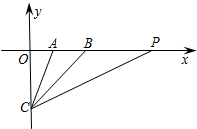 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.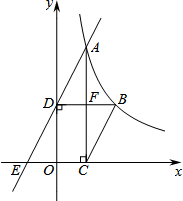 如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.
如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.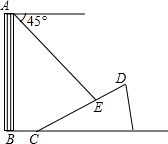 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上一点B在第一象限,函数y=$\frac{k}{x}(x>0)$的图象经过BC边上的点M,且MB=2MC,若矩形OABC的面积为6,则k的值为2.
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上一点B在第一象限,函数y=$\frac{k}{x}(x>0)$的图象经过BC边上的点M,且MB=2MC,若矩形OABC的面积为6,则k的值为2.