题目内容
13.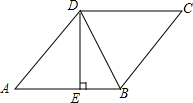 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | 10$\sqrt{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 首先设菱形ABCD边长为x,则AE=x-2,根据三角函数定义可得$\frac{x-2}{x}$=$\frac{3}{5}$,再解即可得到x的值,然后利用勾股定理计算出DE的长,然后在根据正切定义可得tan∠DBE的值.
解答 解:设菱形ABCD边长为x,
∵BE=2,
∴AE=x-2,
∵cosA=$\frac{3}{5}$,
∴$\frac{AE}{AD}$=$\frac{3}{5}$,
∴$\frac{x-2}{x}$=$\frac{3}{5}$,
∴x=5,
∴AE=5-2=3,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=4,
∴tan∠DBE=$\frac{DE}{BE}$=$\frac{4}{2}$=2.
故选:B.
点评 本题考查了菱形的性质,以及三角函数的应用,要熟练掌握好边角之间的关系,菱形四边相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列图形中,既是轴对称又是中心对称图形的是( )
| A. | 正五边形 | B. | 等腰梯形 | C. | 平行四边形 | D. | 圆 |
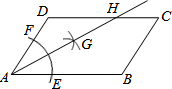 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③. (1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.
(1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.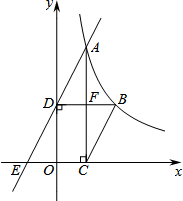 如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.
如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.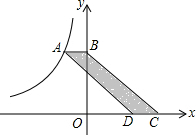 如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.
如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.