题目内容
18.有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球,则摸出的两个球号码之和等于3的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 采用树形图法(或列表法)列出两次摸球出现的所有可能结果,让摸出的两个球号码之和等于5的情况数除以总情况数即为所求的概率.
解答 解:根据题意,可以画出如下的树形图: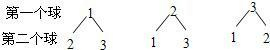
从树形图可以看出,摸出两球出现的所有可能结果共有6种;
设两个球号码之和等于3为事件A,
摸出的两个球号码之和等于5的结果有2种,
它们是:(1,2)(2,1),
∴P(A)=$\frac{2}{6}$=$\frac{1}{3}$.
故选B.
点评 本题考查借助树状图或列表法求概率.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
8.掷一枚质地均匀的硬币5次,下列说法正确的是( )
| A. | 必有5次正面朝上 | B. | 掷2次必有1次正面朝上 | ||
| C. | 不可能5次正面朝上 | D. | 可能有2次正面朝上 |
13.下列事件中是随机事件的是( )
| A. | 测量某天的最低气温,结果是-150℃ | |
| B. | 三角形内角和等于180° | |
| C. | 随意翻一本书的页码,这页的页码是奇数 | |
| D. | 通常加热到100℃时,水沸腾 |
10.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | x2+y2=(x+y)(x-y) | C. | (a+4)(a-4)=a2-16 | D. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 |
8.三角形的高线是( )
| A. | 直线 | B. | 线段 | C. | 射线 | D. | 三种情况都有 |
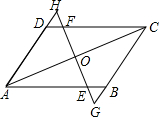 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.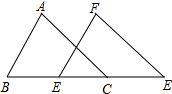 如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE. 如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.
如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.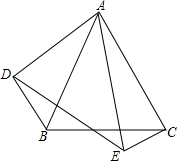 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.