题目内容
17.解方程组(1)$\left\{\begin{array}{l}{3x-2y=6}\\{2x+3y=17}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-2(2y+1)=4}\\{x+\frac{2y+1}{2}=4(x-1)}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-2y=6①}\\{2x+3y=17②}\end{array}\right.$,
①×3+②×2得:13x=52,即x=4,
把x=4代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x-4y=6①}\\{6x-2y=9②}\end{array}\right.$,
②×2-①得:9x=12,即x=$\frac{4}{3}$,
把x=$\frac{4}{3}$代入①得:y=-$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{1}{2}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
8.掷一枚质地均匀的硬币5次,下列说法正确的是( )
| A. | 必有5次正面朝上 | B. | 掷2次必有1次正面朝上 | ||
| C. | 不可能5次正面朝上 | D. | 可能有2次正面朝上 |
5.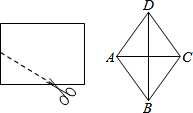 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )| A. | 10 | B. | 20 | C. | 40 | D. | 80 |
12.已知方程组$\left\{\begin{array}{l}{5x+y=3}\\{ax+5y=4}\end{array}\right.$和$\left\{\begin{array}{l}{x-2y=5}\\{5x+by=1}\end{array}\right.$有相同的解,则a,b的值为( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-4}\\{b=-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-6}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=14}\\{b=2}\end{array}\right.$ |
2. 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )| A. | 折扇大 | B. | 团扇大 | C. | 一样大 | D. | 不能比较 |
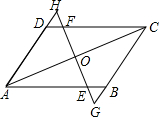 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.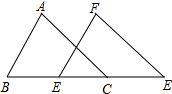 如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.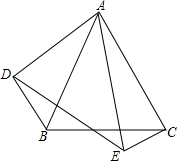 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.