题目内容
5.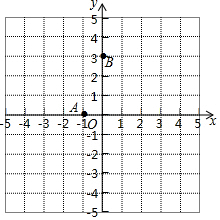 (尺规作图)已知在平面直角坐标系中,A(-1,0),B(0,3),在坐标轴(x轴和y轴)上找出一点C,使 A、B、C三点围成的三角形是等腰三角形,请找出所有满足条件的点.并根据你所找出的点,总结规律.
(尺规作图)已知在平面直角坐标系中,A(-1,0),B(0,3),在坐标轴(x轴和y轴)上找出一点C,使 A、B、C三点围成的三角形是等腰三角形,请找出所有满足条件的点.并根据你所找出的点,总结规律.
分析 根据勾股定理求得AB的长,然后分三种情况讨论得到点C的坐标.
解答 解:如图,点C1、C2、C3、C4、C5、C6即为所求点,
由以上作图可知,点C1、C2、C3是以A为圆心,AB=$\sqrt{10}$为半径的圆与坐标轴的交点,
点C4、C5是以点B为圆心、AB为半径的圆与坐标轴的交点,
点C6、C7是AB中垂线与x坐标轴的交点.
点评 本题考查了等腰三角形的性质及坐标与图形性质,做题时需注意两点,一是注意点C必须位于坐标轴上,二是注意不能漏解,应分AB为底边和腰两种情况分别解答,难度适中.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.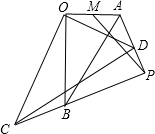 如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
 如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
14.下列方程中是关于x的一元二次方程的是( )
| A. | x2+2x=x2-1 | B. | x3+2x2+3=0 | C. | x(x-1)=1 | D. | 3x2-2xy-5y2=0 |
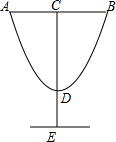 设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11.
设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11.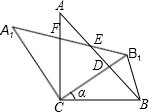 如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.