题目内容
1.若方程2kx(x-2)-x(x+3)+2k+5=0有实数根,则k的取值范围是k≤$\frac{29}{8}$.分析 首先整理方程得(2k-1)x2-(4k+3)x+2k+5=0,再分类讨论:若2k-1=0,而-(4k+3)≠0,原方程变为一元一次方程,有解;当2k-1≠0,且△≥0,即△=(4k+3)2-4(2k-1)(2k+5)=-8k+29≥0,方程有实数根,得到k≤$\frac{29}{8}$且k≠$\frac{1}{2}$,最后综合得到k的取值范围
解答 解:原方程整理得(2k-1)x2-(4k+3)x+2k+5=0,
当2k-1=0,即k=$\frac{1}{2}$,并且-(4k+3)≠0,所以原方程变为一元一次方程,有解,满足条件;
当2k-1≠0,且△≥0,即△=(4k+3)2-4(2k-1)(2k+5)=-8k+29≥0,方程有实数根,
解两个不等式得k≤$\frac{29}{8}$且k≠$\frac{1}{2}$;
综上所述,k的取值范围为k≤$\frac{29}{8}$.
故答案为:k≤$\frac{29}{8}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元一次方程和一元二次方程的定义以及分类讨论思想的运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
11.一名射击爱好者7次射击的中靶环数如下(单位:环):7,10,9,8,7,9,9,这7个数据的中位数是( )
| A. | 7环 | B. | 8环 | C. | 9环 | D. | 10环 |
12.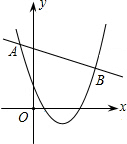 已知二次函数${y_1}=a{x^2}+bx+c$(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(-2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )
已知二次函数${y_1}=a{x^2}+bx+c$(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(-2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )
 已知二次函数${y_1}=a{x^2}+bx+c$(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(-2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )
已知二次函数${y_1}=a{x^2}+bx+c$(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(-2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )| A. | x<-2 | B. | x>8 | C. | -2<x<8 | D. | x<-2或x>8 |
6.已知a为任何实数,那么下列各式一定有意义的是( )
| A. | $\sqrt{{a}^{2}-1}$ | B. | $\sqrt{{a}^{2}+1}$ | C. | $\sqrt{\frac{1}{(a-1)^{2}}}$ | D. | $\sqrt{\frac{1}{(a+1)^{2}}}$ |
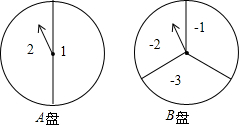 如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y)
如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y) 三角形的顶点坐标分别是A(2,2),B(4,2),C(6,4),试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.画出图形并写出各点的坐标.
三角形的顶点坐标分别是A(2,2),B(4,2),C(6,4),试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.画出图形并写出各点的坐标.