题目内容
10.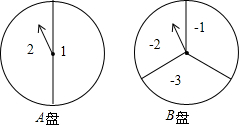 如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y)
如图有两个可自由转动的转盘,A转盘被平均分成2个相等的扇形区域,分别标注数字1和2;B转盘被平均分成3个相等的扇形区域,分别标注数字-1,-2,-3.分别转动这两个转盘,将A盘所得结果记为x,B盘所得结果记为y,这样就确定了点P的坐标(x,y)(1)用列表或树状图法写出点P的所有可能性;
(2)求点P落在直线y=2x-5上的概率.
分析 (1)首先根据题意列出表格或画出树状图,然后由表格或树状图即可求得所有等可能的结果;
(2)首先根据(1)中的树状图或表格求得点P落在直线y=2x-5上的情况,然后利用概率公式求解即可求得答案.
解答 解:(1)列表得:
| A盘(x) B盘(y) | 1 | 2 |
| -1 | (1,-1) | (2,-1) |
| -2 | (1,-2) | (2,-2) |
| -3 | (1,-3) | (2,-3) |

则点P的所有可能性有:(1,-1),(1,-2),(1,-3),(2,-1),(2,-2),(2,-3);
(2)∵点P落在直线y=2x-5上的有(1,-3)与(2,-1)两种情况,
∴点P落在直线y=2x-5上的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
18.3的倒数是( )
| A. | $\frac{3}{1}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -3 |
2.解方程:$\frac{4}{4{x}^{2}-1}$-$\frac{2}{2x-1}$=0.x=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 无解 |
19.下列运算正确的是( )
| A. | |-6|=6 | B. | $(\frac{1}{2})^{-1}=-2$ | C. | $\sqrt{16}=±4$ | D. | a2•a3=a6 |
20. 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
(1)填空:x=60,y=80;
(2)在扇形统计图中,C部分所对应的扇形的圆心角是144度;
(3)根据抽样调查结果,请估计该校学生一年阅读课外书20本以上的学生人数.
 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
(2)在扇形统计图中,C部分所对应的扇形的圆心角是144度;
(3)根据抽样调查结果,请估计该校学生一年阅读课外书20本以上的学生人数.