题目内容
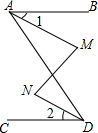 如图,AB∥CD,∠M=∠N,求证:∠1=∠2.
如图,AB∥CD,∠M=∠N,求证:∠1=∠2.考点:平行线的判定与性质
专题:证明题
分析:根据平行线的性质得出∠ABD=∠ADC,根据平行线的判定得出AM∥DN,根据平行线的性质得出∠MAD=∠NDA,即可得出答案.
解答:
证明:∵AB∥CD,
∴∠ABD=∠ADC,
∵∠M=∠N,
∴AM∥DN,
∴∠MAD=∠NDA,
∴∠BAD-∠MAD=∠ADC-∠NDA,
∴∠1=∠2.
∴∠ABD=∠ADC,
∵∠M=∠N,
∴AM∥DN,
∴∠MAD=∠NDA,
∴∠BAD-∠MAD=∠ADC-∠NDA,
∴∠1=∠2.
点评:本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
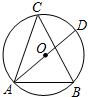 郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
郑州某小区新建一个圆形人工湖,如图所示,弦AB是湖上一座桥,已知桥AB长为200米,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )A、100
| ||
B、200
| ||
C、300
| ||
D、400
|
将抛物线y=ax2-1(a≠0)的图象向左平移2个单位后,所得抛物线经过(1,-4)点,则a等于( )
A、-
| ||
| B、-1 | ||
| C、-3 | ||
| D、-5 |
若被除式是五次三项式,除式是三次单项式,则商式是( )
| A、五次三项式 |
| B、四次三项式 |
| C、三次三项式 |
| D、二次三项式 |
下列说法中不正确的是( )
| A、全等三角形的周长相等 |
| B、全等三角形的面积相等 |
| C、全等三角形一定能够重合 |
| D、全等三角形一定关于某直线对称 |
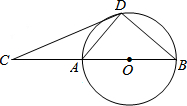 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 如图所示,OA=OB,∠O=60°,AC=OD,∠OAD=25°.求∠ACB的度数.
如图所示,OA=OB,∠O=60°,AC=OD,∠OAD=25°.求∠ACB的度数. 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.