题目内容
 如图所示,OA=OB,∠O=60°,AC=OD,∠OAD=25°.求∠ACB的度数.
如图所示,OA=OB,∠O=60°,AC=OD,∠OAD=25°.求∠ACB的度数.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:连接AB,得出等边三角形OAB,求出∠CAB=∠O=60°,OA=AB,根据SAS推出△OAD≌△ABC,根据全等三角形的性质推出∠ACB=∠ODA即可.
解答:
解:连接AB,
∵OA=OB,∠O=60°,
∴△OAB是等边三角形,
∴∠CAB=∠O=60°,OA=AB,
在△OAD与△ABC中,
,
∴△OAD≌△ABC(SAS),
∴∠ACB=∠ODA=180°-∠O-∠OAD=180°-60°-25°=95°.

∵OA=OB,∠O=60°,
∴△OAB是等边三角形,
∴∠CAB=∠O=60°,OA=AB,
在△OAD与△ABC中,
|
∴△OAD≌△ABC(SAS),
∴∠ACB=∠ODA=180°-∠O-∠OAD=180°-60°-25°=95°.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS,全等三角形的对应角相等,对应边相等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )
如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )| A、70° | B、60° |
| C、55° | D、45° |
抛物线y=ax2+bx+c(a≠0)的对称轴是x=3,且经过点(5,0),则a+b+c等于( )
| A、0 | B、1 | C、3 | D、5 |
若不等式(a+1)x>2的解集为x<
,则a的取值范围是( )
| 2 |
| a+1 |
| A、a<1 | B、a>1 |
| C、a<-1 | D、a>-1 |
 如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?
如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?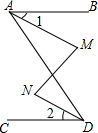 如图,AB∥CD,∠M=∠N,求证:∠1=∠2.
如图,AB∥CD,∠M=∠N,求证:∠1=∠2. 如图,∠1+∠C=100°,∠2+∠B=100°,AB与CD平行吗?说明你的理由.
如图,∠1+∠C=100°,∠2+∠B=100°,AB与CD平行吗?说明你的理由.